제어공학개론 강의에서는 행렬-벡터 및 행렬-행렬 곱셈의 전개, 선형 방정식의 해의 존재성과 유일성, 행렬의 역수, 슈르 여인수, 고유값 및 고유벡터, 대각화 조건 등을 다루며, 특히 대각화가 가능한 조건과 제어 이론에서의 응용에 대해 설명합니다.

제어공학에서 전달 함수(T.F)를 상태 공간(S.S) 표현으로 변환하는 방법을 설명하며, 예시로 주어진 T.F를 통해 상태 공간 표현의 행렬 A, B, C, D를 도출합니다. 또한, 분자 다항식이 포함된 경우와 몫이 있는 경우의 처리 방법을 다루고, 행렬의 전치가 T.F에 미치는 영향을 설명합니다.

제어공학의 상태공간 표현과 전달함수 변환에 대한 강의에서는 비선형 시스템의 선형화, 컴퓨터의 미분 방정식 해결 방법, 상태공간 표현을 라플라스 변환하여 전달함수를 도출하는 과정이 설명된다. 전달함수는 시간 불변 시스템에만 적용 가능하며, 임펄스 응답에 대한 초기값도 다루어진다.

제어공학 개론에서는 안정적인 전달 함수, 정상 상태 응답, 보드 플롯 및 상태 공간 표현에 대해 설명합니다. 안정적인 전달 함수는 모든 극의 실수부가 음수여야 하며, 정상 상태 응답은 입력 신호에 의해 발생합니다. 보드 플롯은 주파수에 따른 전달 함수의 진폭과 위상을 시각화하며, 로그 스케일을 사용하여 저주파와 고주파를 효과적으로 표현합니다. 비선형 ...

머신러닝의 결정 트리 알고리즘은 데이터를 분할하기 위해 정보 엔트로피, 이득 비율, 지니 지수를 사용하며, 과적합 문제를 해결하기 위해 전후 가지치기를 적용합니다. 연속 값과 결측값 처리 방법도 설명되며, 다변량 결정 트리의 가능성에 대해서도 논의됩니다.

머신러닝의 결정 트리 알고리즘은 데이터를 분할하기 위해 정보 엔트로피, 이득 비율, 지니 지수를 사용하며, 과적합 문제를 해결하기 위해 전후 가지치기를 적용합니다. 연속 값과 결측값 처리 방법도 설명되며, 다변량 결정 트리의 가능성에 대해서도 논의됩니다.

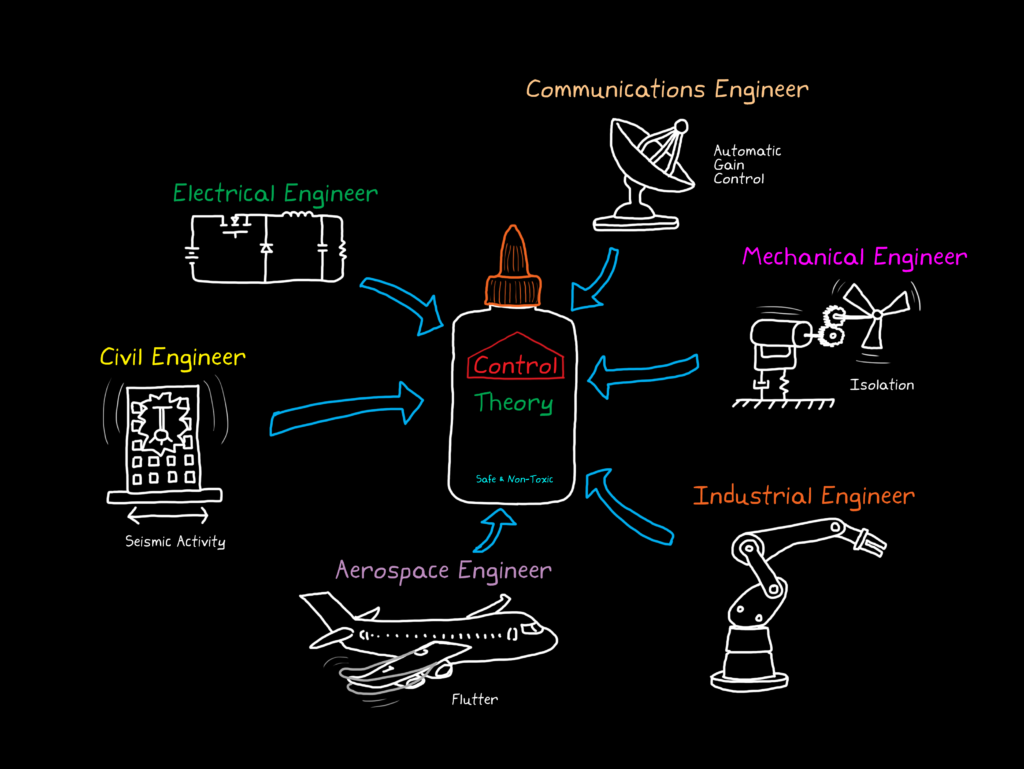
제어공학개론의 첫 수업에서는 제어의 정의와 과정, 예시로 드론을 통해 입력 설계의 필요성을 설명했습니다. 제어 시스템은 입력과 출력의 관계를 모델링하고, 피드백을 통해 외란을 줄이며 시스템의 강인성과 동적 특성을 개선합니다. 다음 포스트에서는 다양한 모델링 방법에 대해 다룰 예정입니다.

제어공학개론의 첫 수업에서는 제어의 정의와 과정, 예시로 드론을 통해 입력 설계의 필요성을 설명했습니다. 제어 시스템은 입력과 출력의 관계를 모델링하고, 피드백을 통해 외란을 줄이며 시스템의 강인성과 동적 특성을 개선합니다. 다음 포스트에서는 다양한 모델링 방법에 대해 다룰 예정입니다.