[Review] K-UNN : k-space interpolation with untrained neural network
Challenge 당시 논문 리딩 요약으로, 얄팍한 지식으로 겉핥기 식으로 요약한 것이라 틀린 정보, 추측성 문장 많음.
https://arxiv.org/abs/2208.05827
MRI 문제에 대한 큰 2가지 방법론 : U-net과 같이 image space 에서의 Convolutional Neural Network, k-space 도메인에서 수학적 최적화 문제를 해결하는 방법.
이러한 방법을 k-space interpolation이라고 부르며, 해당 문제에 대한 가장 기초적이고 좋은 솔루션을 주는 것이 GRAPPA임. Low freq 영역에서 masking되지 않은 부분을 이용하여 weight를 구하고, masking 된 High freq 부분을 채워넣는. 선형대수를 이용하므로 interpolation이라는 이름이 붙어도 무방한 것 같다.
교수님께서도 k-space에서 문제를 해결하는게 좋아보인다고 말씀하시기도 했고, 기존에 주어진 varnet의 경우도 결국 corrector의 역할을 하는 부분은 u-net이라 비효율적이어 보임. 이 논문의 경우 애초에 k-space에서 역행렬을 구해 문제를 해결하되, weight를 주는 행렬인 A행렬이 ill-conditioned라는 것을 이용하여 (반대로 데이터가 sparse하다는걸 이용하여) 특정 weight들을 ground truth로 mapping하는 행렬을 UNN(untrained neural network)으로 훈련하는 방법을 제시함.
https://kr.linkedin.com/pulse/random의-재발견-압축센싱compressed-sensing-gromit-park
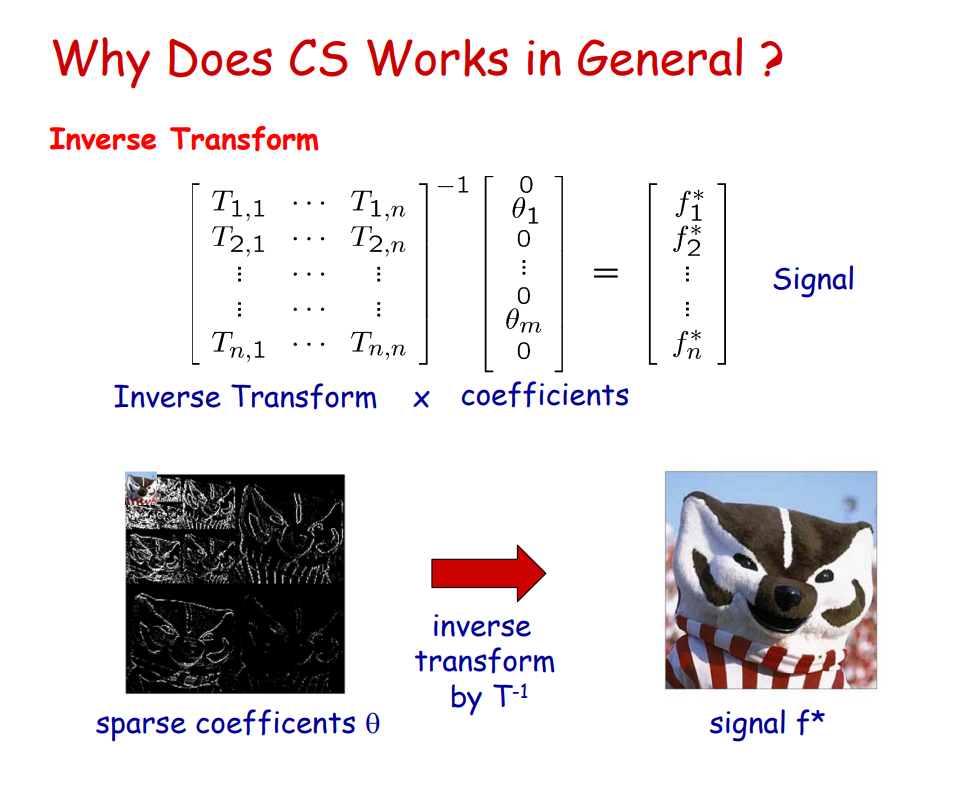
CS : Compressed Sensing - 정말 적은 sampling(대신 랜덤이어야 함) 만으로 얼추 비슷하게 recovery 하는 방법. 기본적으로 Nyquist samping theorm에 기반을 두고 있는데, 훨씬 적은 방식으로 유사한 시그널을 만들어낼 수 있다는 것이 장점임.
\[Ax=y\]x가 weight에 해당하고, y가 데이터에 해당. A (sparse mapping matrix)를 알아내는게 목적.
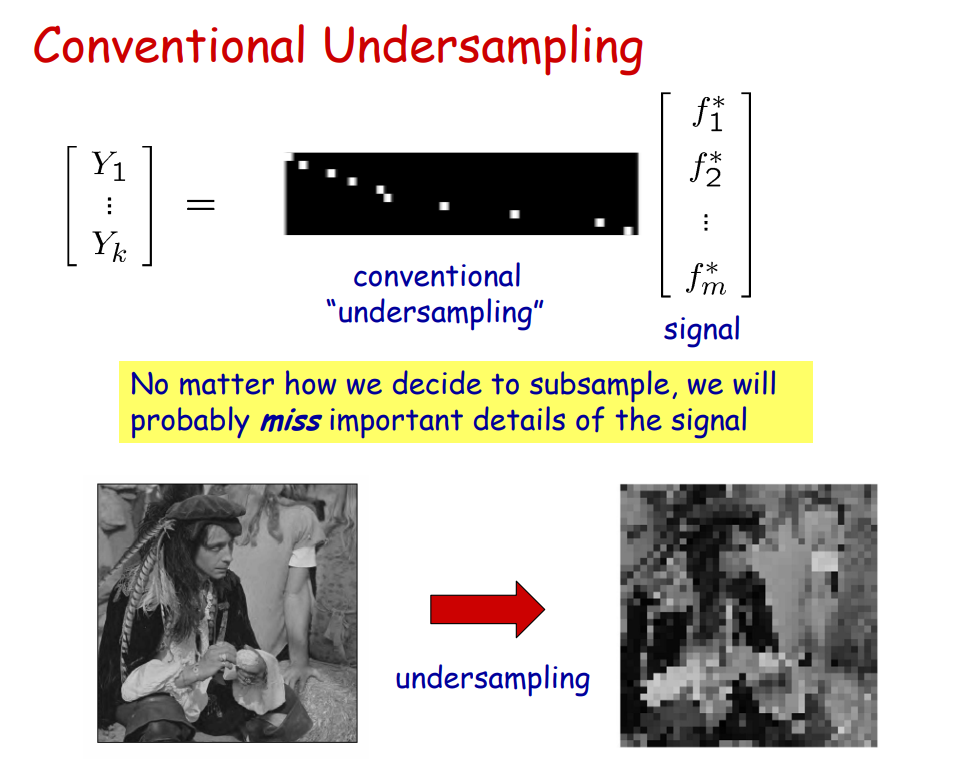
y, 즉 sampling data를 full freq에서 sampling 할 경우 vs random(compressive) sampling 할 경우
CS 설명 : https://www.cs.jhu.edu/~misha/ReadingSeminar/Papers/Baraniuk06.pdf, https://kr.linkedin.com/pulse/random의-재발견-압축센싱compressed-sensing-gromit-park
쉽게 말하면 equal freq 간격으로 n개의 freq 데이터를 sampling하는 대신 KxN matrix T를 곱하여 k개의 undersampled data만 사용.
원래의 signal (f)는 IFFT를 통해 재구성해낼 수 있음.
위 식을 다음과 같이 표현할 수 있음
\[y=\phi x = \Phi T^{-1}\alpha\]general undersampling에 비해서 random sampling이 훨씬 더 많은 데이터를 가지고 있음을 알 수 있음.
CS 방법은 Data Augmentation에도 활용될 여지가 있을 것으로 보인다. Masking에 비해 훨씬 더 많은 정보를 가지고 있기 때문.
\[\min_{\xi} \frac{1}{2}||A\Psi(\xi)-y||_1^2 + \lambda||\xi||_1\]$\xi = \alpha$이며, 1-norm을 사용하는 이유는 $\xi$가 sparse encoding matrix이기 때문.
해당 논문에서는
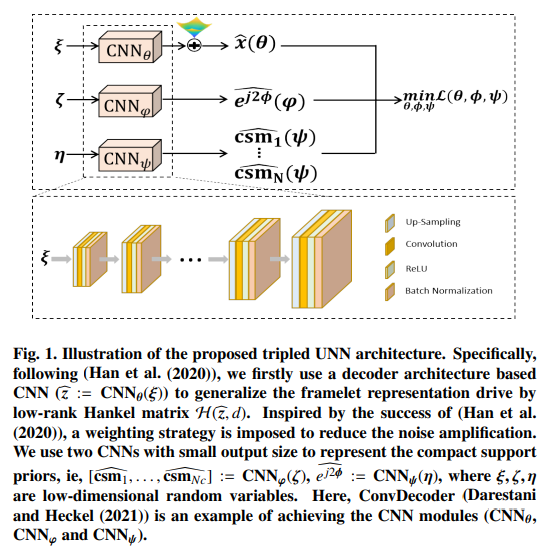
\[x=\Phi(\xi)\]이 mapping임을 활용하여 UNN을 이용하여 해당 Mapping을 학습시켜보자는 목적을 가지고 있음.
\[x=\Phi(\zeta), \\ \min_{\Phi} \frac{1}{2} ||A\Phi(\zeta)-y||_1^2\]여기서의 $\zeta$는 UNN의 weight, 으로 알아내야 할 var가 됨.
추가적으로 알아봐야 할 논문/기술들
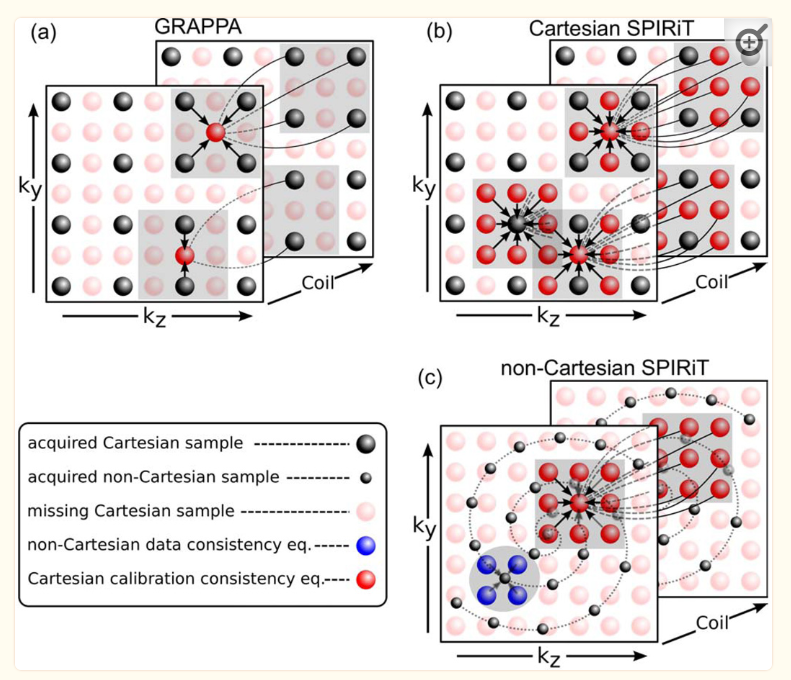
SPIRiT : Iterative Self=consistent Parrel Imaging Reconstruction from Arbitary k-space
ALOHA : multi-channel version SPIRiT
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2925465/
https://mriquestions.com/senseasset.html - SENSE, ASSET (coil sensitivity encoding 관련하여 더 찾아보면 좋을듯)
SPIRit에 관하여 찾아보며 더 알아낸, 것들: SMASH, SENSE (GRAPPA 기술의 시초가 되는 듯 함, Coil sensitivity를 explicit하게 or implicit하게 사용하는지에 따라 나뉨. Multi-coil에 대한 각각의 sensitivity를 사용…
여기는 내가 설명하는것보다 이거 보는게 빠를 것 같아서 썼음.
csm : coil sensitivity map
$\phi$ : image shift at k-space domain? 그냥 페이즈를 주는거라 생각해야할듯
$\theta$ : 아까 말한 CS에서의 data 압축에 관련된 파라미터. 위에서는 $\zeta$
Objective function은
다음으로 요약될 수 잇음. phase 부분은 왜 곱해져 있는지 이해할 수 없네.. 위에 + 하고 gradient같은것도 잘 모르겠음.
수치적 최적화 문제에 NN을 활용한 예시로써도 가치가 있고 어떻게 모델링했는지 보여준다는 면에서도 가치가 있음
겉핥기식이라 애매한 부분이 많긴한데, k-space에서 image-space 활용안하고? 정확히는 활용하는데 매 block마다가 아니라 csm의 fourier transform된거를 학습시키는거라 더 괜찮음.
추가로 csm을 어떻게 얻는지 방식이나, 어떤 식으로 활용되는지도 알아보면 좋을듯 하다