[머신러닝] Chap 2 - 모델 선정과 성능평가

Disclaimer

📣 본 포스트는 조우쯔화의 단단한 머신러닝 책을 요약 정리한 글입니다.

Chap 2. Model selection and Evaluation

2.1 Empirical error and Overfitting

error rate

propotion of incorrectly classified samples $E = a/m$

정밀도

1-Error rate, $1-a/m$

Error

difference beteween the output predicted by learner and ground-truth Learner와 Ground truth값 사이의 차이

training error, empirical error

training set에서 만들어진 error

generalization error

testing set에서 만들어진 error

overfitting

과적합, training data의 특성을 모든 데이터의 일반적 성질로 학습하는 것.

2.2 Evaluation method

Hold-out

• Data set의 일부분을 떼어내서 이를 testing set으로 사용하는 것.
• Hold-out 할 때 나누어지는 set들의 데이터 분포가 같아야 함.

Cross validation

• k개로 나눌 경우 k-fold cross validation이라고 불림
• 서로 겹치지 않는 k개의 set으로 나누고 그 중 하나를 testing set으로, 나머지를 training set으로 하여 k번의 훈련과 테스트를 거침
• 최종 값은 각 테스트의 결과값의 평균으로 함.
• 이를 p번 반복하여 p차 k겹 교차검증 (eg 10차 10겹 교차 검증)을 자주 사용

LOOCV(Leave-One-Out Cross Validation)

• # of data samples가 $m$일 때, $k=m$인 cross validation을 leave-one-out cross validaion이라 함.
• data sample 수 만큼 training, testing을 진행시켜야 함.

Bootstrapping

• Initial data set D에서 중복을 허용하여1개씩 뽑아 D의 크기만큼 뽑는다.
• 즉 $D={1, 2, 3, 4}$라면, $D’={1,1,2,4}$ 인 것이다.
• 수학적으로 ,

\[\lim\limits_{m\rightarrow \infty} \bigg(1-\frac{1}{m}\bigg)^m = \frac{1}{e}\approx 0.368\]

• 즉 36.8%의 sample은 $D’$에 담기지 않게 됨. 즉 이 집합($D-D’$)을 testing set으로 하고 D’을 training set으로 활용하는 것을 Out-of-Bag 예측이라 부름.

Parameter tuning

validation set

파라미터 튜닝을 위해 testing set을 거치기 전에 미리 모델 평가 및 선택 과정에서 쓰는 평가 데이터 집합

2.3 모델 성능 측정

• 평균제곱오차 (MSE, mean squared error) :

\[E(f;D) = \frac{1}{m} \sum_{i=1}^m (f({\bf x_i})-y_i)^2\]

확률 밀도 함수로 표현하면,

\[E(f;D) = \int_{x\sim D} (f({\bf x})-y)^2 p({\bf x} ) d({\bf x})\]

• 오차율, 정확도

\[E(f;D) = \frac{1}{m} \sum_{i=1}^m II(f({\bf x_i})\neq y_i)\]

정확도는 1-오차율,

\[acc(f;D) = \frac{1}{m} \sum_{i=1}^m II(f({\bf x_i})= y_i)\]

확률밀도함수로 나타낸 경우에도 MSE에서 나타낸 것과 동일하게 나타낼 수 있음.

Confusion matrix

• True/False : 실제 값과 예측 값이 일치하는지
• Positive/Negative : 예측한 값이 양성인지 음성인지

Instruction :

1. P, N을 먼저 생각한다. ex) FN이면, 일단 Negative이므로 예측은 negative임.
2. 이제 T, F를 생각한다. F이므로, negative와 반대인 positive가 ground truth임을 알 수 있음.

• Confusion matrix : TP, FN, FP, TN을 각각 matrix에 나타낸 것.

실제 값 : 예측값	양성	음성
양성	TP	FN
음성	FP	TN

• TP(true positive) : A를 A라고 예측한 것
• TN(true negative) : ~A를 ~A라고 예측한 것
• FP(false positive) : ~A를 A라고 예측한 것
• FN(false negative) : A를 ~A라고 예측한 것

단 binary classification이 아닌 경우에도 confusion matrix를 적용할 수 있음.

ground truth : prediction	A	B	C	D
A	9	1	0	0
B	1	15	3	1
C	5	0	24	1
D	0	4	1	15

• 정확도(accuracy) in confusion matrix :

\[acc = \frac{TP+TN} {TP+TN+FP+FN}\]

• Multiclass의 경우 diagonal(only true positive)만을 모두 더해 m으로 나눈 값을 의미
• 위 예시에서의 정확도는 $(9+15+24+15)/80 = 0.78$

Precision

• 정밀도. positive라고 예측한 것 들 중 실제로 positive인 것들의 빈도

\[prec = \frac{TP} {TP+FP}\]

Recall

• 재현율. ground truth가 positive인 것들 중 모델이 positive라고 예측한 것의 빈도

\[rec = \frac{TP} {TP + FN}\]

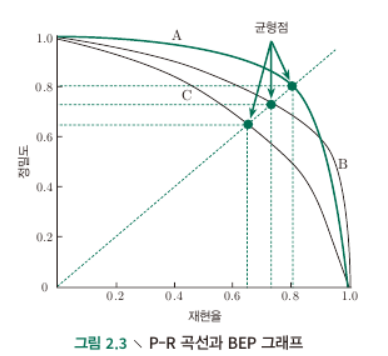
P-R Curve, AUPRC

• Precision과 Recall은 일종의 tradeoff가 존재함.
• Precision을 y축에, Recall을 x축에 두고 그래프를 만든 것이 P-R curve임.
• threshold를 점차 바꾸어 가며, 각각의 confusion matrix로부터 (P, R)을 구하는 방법을 이용.

• BEP (Break-Even Point)

  $y=x$와 PR curve가 만나는 점, PR curve 가 intersect할 경우 평가하는 방법중 하나.

• 일반적으로 Area Under (PR) Curve (AUPRC)가 큰 classifier를 좋은 classifier라고 봄.
• 그러나 PR curve 간에 cross가 일어나는 경우에는 AUC만으로 비교하기가 애매함.
• P, R의 정의에 의해서 AUC=1인, 1x1의 square 형태로 나타나는 것이 가장 이상적임.
• $(1, 1)$에 가장 가까운 threshold를 고르는 것이 이상적.

F1-score

• 정밀도, 재현율 두 값을 조화 평균하여 하나의 수치로 나타낸 지표
• 정밀도($P$), 재현율($R$)라 할 때

\[\text{F1 score = } \frac{2PR}{P+R}\]

F-beta-score

• F1-score는 Precision, Recall의 가중치를 동일하게 둔 경우이며, 실제 상황에서 어느 특정 값에 가중치를 두어야 할 경우 F-beta score를 사용함. $\beta>1$인 경우는 $R$의 영향이 더 크며, $\beta<1$의 경우는 $P$의 영향이 더 큼.

\[F_\beta = \frac{(1+\beta^2)\times P \times R} {(\beta^2\times P) + R}\]

(Macro, Micro) P, R, F1-score

• 여러 개의 혼동 행렬을 얻게 될 경우, 각 Confusion matrix에서 얻은 P, R, F1값들을 계산하고 이 값들을 평균한 것이 macro-P, macro-R, macro-F1 이라 한다.
• 반대로 각각의 혼동행렬이 대응하는 원소들에 대한 TP, FP, TN, FN들의 평균값을 구하고 이를 이용하여 P, R, F1값을 계산하면 이를 micro-P, micro-R, micro-F1이라 한다.

ROC, AUC

• threshold를 정하기 위한 도구 : ROC

\[TPR = \frac{TP}{TP+FN}\] \[FPR = \frac{FP}{TN+FP}\]

• True Positive Rate (TPR)

  ground truth가 True인 것 들 중에서 classifier가 실제로 True라고 한 것의 비율 (Recall)

• False Postive Rate (FPR)

  ground truth가 false인 것 들 중에서 classifier가 실제로 False라고 한 것의 비율

• TPR을 y축, FPR을 x축에 놓고 그래프로 표현하 것이 RPC 그래프
• y=x는 랜덤 예측 모델의 경우일 것이며, AUC가 클 수록 더 좋은 모델임.
• AUC는 순서 예측 품질, 즉 순서의 loss와 큰 관련이 있음 $AUC=1-l_{rank}$

Cost-sensitive error rate, cost curve

• FN, FP가 서로 다른 cost를 가지는 경우 unequal cost라는 개념 적용가능.
• 도메인 지식에 기반으로 cost matrix를 생성

실제 값 : 예측값	양성	음성
양성	0	$cost_{01}$
음성	$cost_{10}$	0

• 비균등 비용에서는 오차 횟수의 최소화가 아닌 비용(total cost)의 최소화를 목적으로 하므로, cost-sensitive error rate는 다음과 같이 정의된다.

\[\begin{aligned}E(f;D;cost) = \frac{1}{m}\bigg(\sum_{{\bf x_i}\in D^+}\text{II}(f({\bf x_i})\neq y_i) \times cost_{01}+ \\ \sum_{{\bf x_i}\in D^-}\text{II}(f({\bf x_i})\neq y_i) \times cost_{10}\bigg)\end{aligned}\]

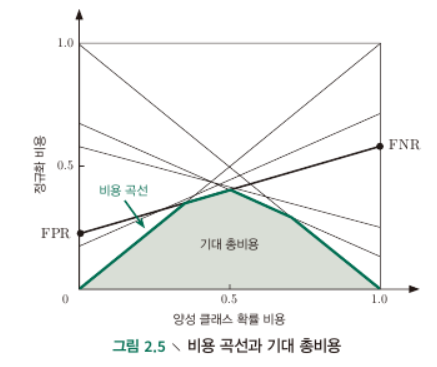
Cost curve

• x axis of cost curves is probability cost of positive class

\[P(+)cost = \frac{p \times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}\]

• $p\in [0,1]$ 는 sample이 positive일 확률. $p=0$일 때 $P(+)cost =0$이고, 1일 때 1이니 비용가중(비용을 고려한) sample이 positive할 확률 을 x축에 놓았다고 볼 수 있음.
• y axis is normalized cost which takes values from [0,1]

\[cost_{norm} = \frac{FNR \times p \times cost_{01} + FPR \times (1-p)\times cost_{10}} {p\times cost_{01} + (1-p)\times cost_{10}}\]

• 내가 p의 확률에 따라 분류한 것이 다 틀렸을 때의 전체 cost를 분모로, p의 확률로 분류하나 FNR, FPR을 고려하여 분류했을 때의 cost를 분자로 하는느낌? 최악의 경우의 최대 cost 분에 현재 학습기의 cost를 normalized cost라고 하는 듯
• $FNR = 1-TPR$
• $p=0$일 때의 $cost_{norm}=FNR$, $p=1$일 때의 $cost_{norm} = FPR$이므로, cost-plane 상에 각각의 ROC curve 의 점들에 대한 $(0,FPR), (1,1-TPR)$을 잇는 직선들을 모두 plot 하여 직선들 아래의 면적이 기대 총 비용 (expected total cost)가 될 것.

2.4 학습기 성능 비교 검증

이항 검정 (binomial test)

• $\epsilon\leq\epsilon_0$ 라는 가설을 세우고 $\alpha=0.05$ 등의 significance 하에서 가설을 기각할 수 있는지 확인.
• 해당 오차율($\epsilon_0$)보다 오차율이 클 확률과 $\alpha$와 비교

t-test (여러 test-set에 대한 오차율을 검정할 때)

• k개의 테스트 오차율 $\hat\epsilon_1, \hat\epsilon_2\cdots,\hat\epsilon_k$을 얻는다면, 각각의 평균 오차율 $\mu$와 분산 $\sigma^2$을 얻을 수 있음.
• 이 때 각각의 테스트 오차율이 독립표본이라면 검정통계량은 다음과 같음.

\[\tau_t = \frac{\sqrt k (\mu-\epsilon_0)}{\sigma}\sim t(k-1)\]

• $\alpha$의 significance 하에서, $\mu=\epsilon_0$의 귀무가설을 기각할 수 있는 기각역은 $(-\infty,t_{-\alpha/2}]$, $[t_{-\alpha/2}, \infty)$ 이다.

교차 검증 t-test

• 두 학습기의 오차율이 같다는 귀무가설을 세우고, 동일한 test-set을 사용하여 나온 두 학습기의 오차율의 차($\Delta_i$)를 t-test 한다.

\[\tau_t = \vert\frac{\sqrt{k}\mu}{\sigma}\vert\]

• 같은 방법으로 기각역을 세워 t-test 하면 됨.
• Test 내의 중복 데이터 등이 존재할 경우 오차율이 독립적이지 않으므로, 5 x 2 cross-validation 등을 활용.

5 x 2 cross-validation

• testing set을 5개로 나누고, 각각의 set을 또 2개로 나누어 2-fold cross-validation을 수행한다. 2개의 오차율 차이값이 도출($\Delta_i^1, \Delta_i^2 \text{ for i=1}\cdots 5$)
• 비독립성의 완화를 위해(?) i=1일때의 오차율의 평균을 $\mu$로 활용
• 분산은 각각의 5개에 대한 분산의 합을 이용.

\[\sigma_i^2 = \bigg(\Delta_i^1-\frac{\Delta_i^1+\Delta_i^2}{2}\bigg)^2+\bigg(\Delta_i^2-\frac{\Delta_i^1+\Delta_i^2}{2}\bigg)^2\]

• 이렇게 계산된 T검정통계량은

\[\tau_t = \frac{\mu}{\sqrt{0.2 \sum_{i=1}^5 \sigma_i^2}}\]

맥니마(McNemar) test

• contingency table of two learners

Alg.A : Alg.B	Correct	Incorrect
Correct	$e_{00}$	$e_{01}$
Incorrect	$e_{10}$	$e_{11}$

• 두 학습기의 성능이 동일하다는 것은 $e_{01}=e_{10}$임. 즉 서로 다르게 판별한 개수의 차가 정규분포를 이룰 것이므로,

\[\tau_{\chi^2} = \frac{(\vert e_{01}-e_{10}\vert -1)^2}{e_{01}+e_{10}} \sim \chi^2_1\]

• 위 검정통계량은 자유도가 1인 카이제곱 분포를 따르게 될 것이다

프리드먼(Friedman) test

• 다수의 알고리즘의 Ranking을 매길 때 사용하는 검정방법
• 앞선 검증법들을 이용하여 각 data set, 각 algorithm별 테스트 결과를 얻고 순위를 매김 (단, 성능값이 모두 같다면 평균 값을 매김)
• 각각의 알고리즘의 평균 등수에 대한 평균과 분산을 구할 수 있으며, N개의 data set, k개의 algorithm에 대해

\[\tau_{\chi^2} = \frac{k-1}{k} \cdot \frac{12N}{k^2-1} \sum_{i=1}^k \bigg(r_i-\frac{k+1}{2}\bigg)^2 \sim \chi^2_{k-1}\]

• 위 검정 통계량은 자유도가 k-1인 카이제곱 분포를 사용.
• 프리드먼 검정이 보수적이므로(차이가 없다고 판별할 가능성이 큼) 개선된 프리드먼 검정을 사용.

\[\tau_F = \frac{(N-1)\tau_{\chi^2}}{N(k-1)-\tau_{\chi^2}}\sim F_{k-1, (k-1)(N-1)}\]

• 위 검정 통계량은 자유도 $k-1$, $(k-1)(N-1)$을 따르는 F분포임.

네메니 사후 검정(Nemenyi post-hoc test)

\[CD = q_\alpha \sqrt{\frac{k(k+1)}{6N}}\]

• q : Tukey 분포
• CD 값을 계산하여서 두 알고리즘 성능의 평균값 차이가 해당 수치 이상일 경우 두 알고리즘은 차이가 있다고 볼 수 있음.

2.5 편향과 분산

• $\bf x$ : 테스트 샘플
• $y_D$ : label
• $y$ : ground-truth (실제 데이터 값)
• $f({\bf x}, D)$ : 모델의 예측값
• 알고리즘의 기대 예측값 (예측값의 평균 or 기댓값)

\[\bar f({\bf x}) = E_D[f({\bf x}, D)]\]

• 분산

\[var({\bf x}) = E_D[(f({\bf x}, D)-\bar f({\bf x}))^2]\]

• 노이즈

\[\epsilon^2 = E_D[(y_D-y)^2]\]

• 편향(기대 결괏값과 실제 데이터의 차이)

\[bias^2({\bf x}) = (\bar f({\bf x})-y)^2\]

• 일반 오차(Total error)가 편향, 분산, 노이즈의 합으로 분해될 수 있음.

\[\begin{aligned} Error(f;D) =& E_D [(f({\bf x};D)-y_D)^2]\\ =& E_D[(f({\bf x};D)-\bar f({\bf x})+\bar f({\bf x})-y_D)^2]\\ =& var({\bf x}) + E_D[(\bar f({\bf x})-y_D)^2]\\ &+ E_D[2(f({\bf x};D)-\bar f({\bf x}))(\bar f({\bf x})-y_D)] \\ =& var({\bf x}) + E_D[(\bar f({\bf x})-y+y-y_D)^2] \\ =& var({\bf x})+((\bar f({\bf x})-y)^2+E_D[(y_D-y)^2]\end{aligned}\] \[\therefore Error(f;D) = bias^2({\bf x})+ var({\bf x})+\epsilon^2\]