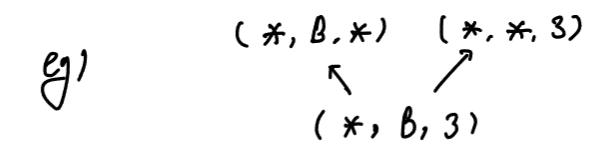[머신러닝] Chap 1 - 서론

Disclaimer

📣 본 포스트는 조우쯔화의 단단한 머신러닝 책을 요약 정리한 글입니다.

Chap 1. 서론

1.2 Machine Learning의 기본 용어

data set

각 사물에 대한 묘사(instance, sample)의 집합

instance, sample

특정 사물에 대한 묘사 (atrribute를 이용하여)

attribute, feature

특정 사물의 속성, 성질

attribute value

그 속성에 대한 속성값

attribute space (sample, input space)

속성들을 공간에 확장시킴

feature vector

특정 sample의 feature들을 space에 나타내었을 때 하나의 sample이 가리키는 vector

Machine Learning

Learn from experience(Data) E, in some tasks T measured by performance measure P

Label

sample의 결과값을 나타내는 정보, label에 따라 문제의 종류가 결정됨

• classsification (분류)

  이산값의 경우 // supervised learning

• regression (회귀)

  연속값의 경우 // supervised learning

• clustering (클러스터링)

  이산값, 분류 기준이 자동적으로 형성 (사전에 알 수 없음) // unsupervised learning

testing

학습으로 만든 모델을 활용하여 예측하는 것. 검증

testing sample (set)

검증에 활용하는 sample들로, training에는 등장하지 않았던 것들

training sample (set)

학습에 사용되는 sample들

• goals of ML : good “generalization” ability. (testing set에서 좋은 성능을 내는 것)
• sample들에 대한 가정 : all samples are i.i.d (independent, identically distributed)
• generally speaking, more sample, the better generalized model

1.3 Hypothesis space

귀납

구체적 사실이나 특수성으로부터 일반성을 찾음.

연역

일반적 법칙, 공리로부터 특수한 정황을 추론

• Machine Learning은 sample을 통해 학습함으로 귀납의 원리를 사용한 귀납 학습(inductive learning) 이라고 할 수 있음.
• attribute를 이용하여 hypothesis space를 구성 가능.

Hypothesis space

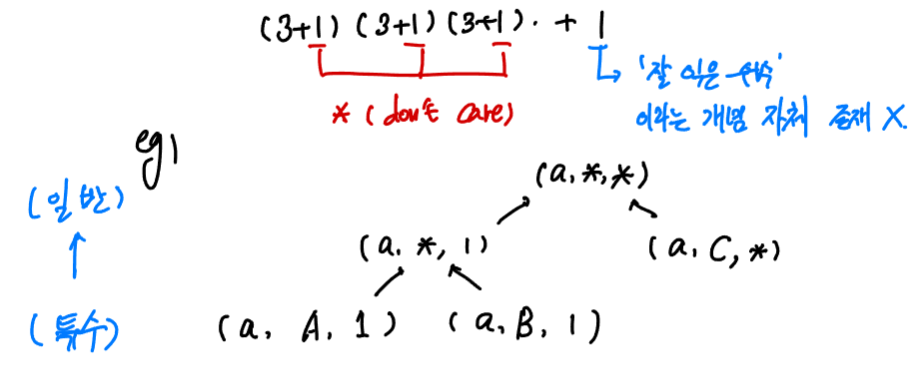
사실상 가능한 모든 가설들의 총집합. attribute 별로 가능한 attribute value의 가짓수 + 1 (don’t care) 를 귀납적으로 나열한 것

• eg) “잘 익은 수박”의 판별을 위해 색깔, 꼭지, 소리라는 attribute로 hypothesis space를 만든다고 가정하자.
  • 각각의 attribute는 3개의 attribute value를 가질 수 있다고 하면, hypothesis space의 크기는 총 $(3+1)\cdot(3+1)\cdot(3+1)+1$ 개일 것이다. 괄호 내에서 하나씩 더해진 1은 “*” 을 나타내는 것으로 don’t care, 해당 attribute는 무관함 마지막의 +1은 ‘잘 익은 수박’이라는 개념 자체가 존재하지 않는 경우에 대한 hypothesis라고 한다.

Version space

너무나 많은 가설들이 training set에 부합할 경우 그 가설들의 집합을 의미함.

1.4 Inductive bias

• 알고리즘이 특정 유형의 가설에 대한 편향을 가질 때 이를 biased라고 한다.
• eg) 비슷한 sample은 비슷한 label이어야 한다라는 bias를 가질 경우
  • A를 B보다 선호하는 편향을 가짐

• eg) 오컴의 면도날 (Occam’s razor)

  더 간단하고 명료한 가설을 선택해야 한다.

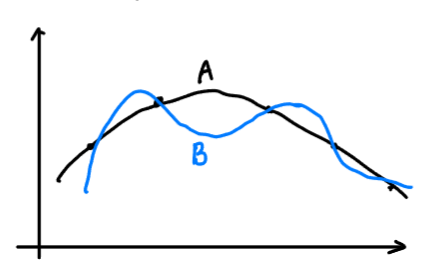
No Free Lunch theorem (NFL)

더 좋은 inductive bias는 없다. (기대 성능은 같다)

pf)

\[\begin{aligned}&\text{let Hypothesis space } \chi \text{ must be discrete} \\ &P({\bf x}) : \text{prob. of samp } {\bf x} \\ &\text{II}(\cdot) : \text{1 if } \cdot \text{ is truth else 0} \\ &P(h \vert X, A_a) : \text{X로 학습한 Algorithm a가 생성한 h의 확률} \\ &f : \text{objective function}\end{aligned}\] \[\begin{aligned}E_{ote}(A_a \vert X, f) =& \sum_h \sum_{x\in \chi-X} P({\bf x}) \cdot \text{II}(h({\bf x})-f({\bf x})) P(h \vert X, A_a)\\ =& \sum_{x\in \chi-X} P({\bf x}) \sum_h P(h \vert X, A_a) \sum_f \text{II}(h({\bf x})-f({\bf x})) \\ =& \sum_{x\in \chi-X} P({\bf x}) \sum_h P(h \vert X, A_a) \cdot \frac{1}{2} \cdot 2^{\vert \chi \vert} \\ =& 2^{\vert \chi \vert - 1} \sum_{x\in \chi-X} P({\bf x})\end{aligned}\]

• $E_{ote}$ is invarient to algorithm
• Learning from NFL theorem : 알고리즘의 좋고 나쁨에 대한 논의는 무의미하다.