[제어공학개론] Lec 17 - PID control

📢Precaution

본 게시글은 서울대학교 심형보 교수님의 23-2 제어공학개론 수업 내용을 바탕으로 작성되었습니다.

Characteristics of PID control

P control

Formula : $u = k_p (r-y(t))$

Example

consider following system

\[\begin{aligned}\dot{x} &= -x + 1 \\r &= 0 \\u &= -k_p x\end{aligned}\]

대입하면,

\[\dot x = -(1+k_p)x+1\]

원래의 $x=1$ 에서 converge한다면, feedback 후에는

$x^T = \frac{1}{1+k_p}$ 에서 수렴하므로 $k_p$가 커짐에 따라 steady-state error는 줄게 됨.

Effect on 2nd order response parameters

• Rise time : decrease
• Overshoot : increase
• Steady-state error : decrease

Differential Equation적 접근

\[\ddot y + 2\xi w_n \dot y + (w_n^2+k_p) y = k_p r\]

2차 시스템 + P controller를 설치한 경우

Steady state라고 하면, dotted 항은 모두 0이 되므로,

\[(w_n ^2 + k_p)y = k_p r\]

$k_p$가 커질 수록 $r, y$의 차이는 작아지며 steady state error는 작아짐을 알 수 있음.

\[r-\frac{r}{w_n^2}>r-\frac{k_p r}{w_n^2+k_p}\]

한편 Feedback system의 새로운 Natural freq $w_n^*$

\[w_n^{*2}=w_n^2+k_p\]

이므로 Natural Frequency도 소폭 커짐을 알 수 있음. 즉 Pole이 살짝 더 negative real part 값이 커지므로 system의 응답속도가 빨라지는(rise time이 줄어드는) 것도 설명 가능.

D control

Formula : $u(t) = K_d e(t)$

현재 값의 변화율을 바탕으로 앞으로의 error의 변화율을 추측해 대응.

그래프 상에서 기울기가 가장 큰 점에서의 negative error 값이 가장 크므로, 가장 크게 break가 걸리게 됨 → overshoot을 줄일 수 있음. (Compared to P control)

S.S. Error에서는 error값이 상수로 변하지 않으므로, steady state error에는 차이를 주지 않음.

Differential Equation적 접근

\[\ddot y + (2\xi w_n+ k_d)\dot y + (w_n^2 + k_p) y = k_p r\]

for 2nd order system. $k_d, k_p$만으로 2nd order system의 pole의 eigenvealue를 바꿀 수 있음.

고전 제어에서는 black box의 문제였으므로(pole placement 등의 method를 알지 못하였으므로,) 경향성만을 이용하여 parameter를 tuning함.

Effect on 2nd order response parameters

• Rise time : small change
• Overshoot : decrease
• Steady-state error : No change

실제 미분 제어의 적용

by laplace transform,

\[U(s) = k_d s E(s)\]

미분기에 해당하는 $s$를 실제 소자들로 구현하기 어렵기 때문에

$\frac{Bs}{s+B}$로 대치하여 사용하게 됨. (Band-Limited Differentiatior)

$B$ : command의 영역으로, $B$값 이상의 frequency에 대해서는 증폭하지 않고, 그 이하의 frequency에 대해서는 $s$의 직선으로 bode plot이 나타나게 됨.

phase plot 또한 $B $ 이전에는 +90도, 이후에는 phase 변화가 없게 되어, low frequency 영역에서는 미분기의 기능을 하고, high frequency(특히 noise가 많은 영역)은 작동하지 작동하지 않도록 구현.

이런식으로 모델링할 경우 passive 소자만으로 만들어낼 수 있다.

Integrator

Formula : $u(t) = \int_0^t (r-y(\tau))d\tau$

아무리 현재의 error의 값이 커도 적분하여 계산되므로 천천히 반응함.

사용하는 유일한 이유 : steady state error를 제거하기 위함.

P 제어, D 제어는 Error=0이 되었을 때 bias에 대한 보상이 0임.

$K_i$는 현재 error가 0이어도 보상이 가능.

Effect on 2nd order response parameters

• Rise time : decrease
• Overshoot : increase
• Steady-state error : 0

Differential Equation

Integration이 포함되었으므로 한번 더 미분해서 나타내면,

\[y^{(3)} + 2\xi w_n \ddot y + w_n^2 \dot y + k_I y = k_I r\]

Example

\[\begin{aligned}y &= x_1 \\\dot{x}_1 &= d + u = d - k_I z \\\dot{z} &= r - y = r - x_1\end{aligned}\]

Equibrilium point

\[\begin{aligned}x_1^* &= r, \quad z^* = \frac{d}{k_I} \\x_1 &\rightarrow r, \quad r - y = r - x_1 = e \rightarrow 0 \\\text{when } z &= z^* = \frac{d}{k_I}, \quad \dot{x}_1 = 0\end{aligned}\]

Physical, Cyber system의 경계는 어디인가

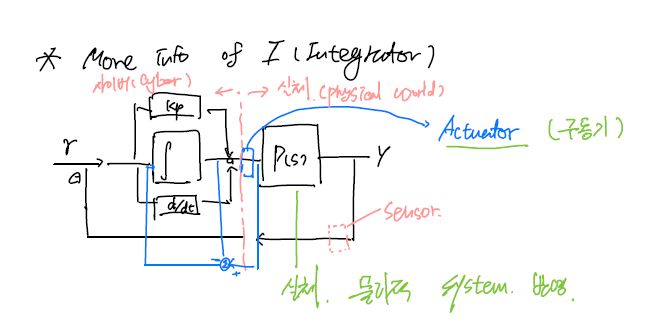
Block diagram에는 반영되지 않았지만, $P(s)$ 앞에 전기 신호를 실제 물리적 힘 등으로 바꾸어 주는 Actuator가 존재. 반대로 $P(s)$에서 나온 결괏값 $y(t)$ 또한 sensor를 통해 sensing 되어 $C(s)$로 Feedback 되어 들어감. 이 때 Actuator, sensor를 우측에 포함하도록 잘랐을 때 우측 부분이 실제 Physical world, 좌측 부분이 Cyber world(컴퓨터 등으로 계산되는) 이라고 할 수 있음.

Saturation

보통 Actuator, sensor는 response가 빠르고 작동범위도 다 작동한다고 가정하지만, 이 또한 입력에 따라 출력을 내는 일종의 system. 작동 범위가 존재함.

특정 출력 이상을 내지 못하고 최대 출력이 정해져있는 saturation이 관찰되기도 함.

Integrator에서 Saturation을 고려해야 하는데, error에 대한 command를 주어도 실제보다 적게 동작하기 때문에 Integrator의 입장에서는 큰 입력을 주었는데도 더 작게 반응하므로 더 큰 입력을 주는 악순환이 시작됨.

이는 Overshoot 값을 크게 만드는 효과가 있음. 즉 Oscillation을 크게 만듦

Anti-windup

windup problem을 해결하기 위해, Actuator를 거친 입력을 sensing하여 바로 integrator에 입력시켜 피드백을 한 번 더 거침

\[u(t) = k_I \int_0^t \bigg(e(s) + k_a \left(u(s)-u_c(s)\right)\bigg)ds\]

$u_c(s)$ : command (Integrator, 다른 제어기들을 거쳐 나온 출력)

$u(s)$ : 실제 Plant에 입력되는 입력(Saturation이 생긴 경우 saturated)

만약 unsaturated situation이라면 원래대로 Integration이 됨.

만약 saturated 된 상황이라면, $k_a$와 곱해지는 괄호 안의 값이 음수가 되어서 더 Overshoot을 증가시키지 않도록 줄여주는 보정을 하게 됨. 즉 $e(s)$의 과대평가를 줄여줌

$k_a$ : Anti-windup gain