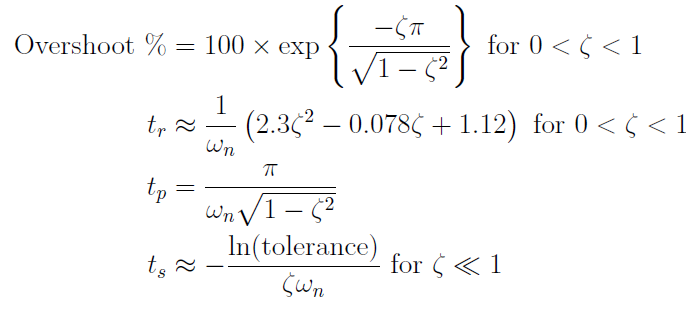[제어공학개론] Lec 16 - Nyquist plot

📢Precaution

본 게시글은 서울대학교 심형보 교수님의 23-2 제어공학개론 수업 내용을 바탕으로 작성되었습니다.

Nyquist Stability Criterion

Open loop 전달함수 $G(s)$의 stability는 pole의 위치를 통해 확인가능하다.

Unity feedback을 적용한 closed loop feedback에서의 stability를 판별하는 방법

Open loop을 전달함수 $G(s)$를 가지고 closed loop을 판별하기.

Contour : Clockwise closed curve

Nyquist Contour : 원점에서 출발, $+\infty j$까지 올라갔다가, 오른쪽으로 돌아 $-\infty j$까지 내려온상태에서 다시 위로 올라오는 시계방향 contour

Nyquist contour위의 점들을 모두 $G(s)$에 대입한 값을 다시 복소평면에 Plot 하면, 마치 복소함수. 이 것이 Nyquist plot임.

Cauchy’s Argument Principle

eg ) $F(s) = (s-a)$

$F(s)$에 어떤 contour를 넣게 되면, Translation이 됨. 점 a이 contour 내부에 존재할 경우

eg ) $F(s) = (s-a)(s-b)$

원점 주위를 2바퀴 도는 모양이 그려짐

eg ) $F(s) = (s-a)(s-b)(s-c)$

점 c는 contour 밖에 있을 때 2바퀴만 돌게 됨

contour 위의 점을 a, b를 시점으로 하는 vector로 보았을 때 contour 주위를 한 바퀴 돈다는 것은, 각도의 입장에서 a에서 1바퀴, b에서 1바퀴, 총 2바퀴를 돈다는 의미가 됨.

contour 밖의 점 c에 대해서는 각도의 변화가 한 바퀴가 아니라 변화가 다시 원점으로 돌아오게 되므로 encirclement와는 관련이 없음

Therefore , # of root of F(s) is inside the contour -> # of rotation(s)

clockwise로 돌면 clockwise방향으로 감싸게 됨

eg ) $F(s) = \frac{1}{(s-a)}$

이 때는 반시계 방향으로 감쌈

Back to the Nyquist Plot…

Considering Transfer function of closed loop, $\text{Denominator } = 1+G(s)$

\[\begin{aligned}G(s) &= \frac{N(s)}{D(s)} \\1 + G(s) &= \frac{D(s) + N(s)}{D(s)}\end{aligned}\]

Let’s Draw Nyquist plot of $1+G(s)$

위의 Cauchy’s Argument principle을 여기다 적용해 보면,

Number of encirclement of zero in counterclockwise = # of unstable pole of $1+G(s) $ - # of unstable zero in $1+G(s)$

\[1+G(s) = \frac{D(s)+N(s)}{D(s)}\]

Denominator of $1+G(s)$ is open loop pole

Numerator of $1+G(s)$ is closed loop pole

그러면 $1+G(s)$ 에 대한 Nyquist plot은 0을 감싸는 횟수로 결정되니까, $G(s)$면 $-1$을 감싸는 횟수로 정하면 되지않나? → Nyquist Theorem

Nyquist Theorem

Nyquist plot of G(s) (open loop system)에 대해,

Number of counter-clockwise encirclements of “$-1$” = $P-Z$

when P := $1+G(s)$ ‘s # of pole in ORHP (open-right half plane) Z := $1+G(s)$’s # of zero in ORHP

왜 “$-1$”만 쓰는가? (unity feedback에 대해서만 Nyquist Theorem이 작동하냐) : 복잡한 system도 unity feedback 형태로 (모든 T.F를 곱해서 )나타낼 수 있으므로 이렇게 고려하는 것.

G(s)가 jw 축에 zero/pole이 있다면?

zero가 있는 경우는 $G(s)$값이 0이니까 0으로 가므로 상관 없음

pole이 있는 경우는 nyquist contour를 살짝 오른쪽으로 이동시켜 pole을 지나가지 않게 한다.

예컨데 $r=\epsilon$ 인 우반원 궤적을 지나도록..

하게 되면, Magnitude의 변화는 없고 (해당 pole을 제외한 다른 pole/zero로부터 의 각도 변화는 매우 미미하므로) Angle이 +90도에서 -90도가 됨 : Clockwise 반바퀴를 돌게 됨.

만약 Double pole이라면 시계 방향으로 한바퀴를 삥 돌게 되므로, -1 을 추가해 주면 됨.

Nyquist plot의 특징

Re축을 기준으로 중심 대칭임

$R=\infty$인 contour에 대해서는 한 점으로 찍힘

Because $G(jw) / G(-jw) = \bar{G(jw)}$이므로

Plot이 “$-1$”을 지난다 : $1+G(\bar s) = 0$이 된다는 의미이고, 이는 $D(\bar s) + N(\bar s) = 0$ : closed loop system의 pole이 $j\omega$에 있음을 의미. (이를 안정하다고 보는 것은 해석의 영역, 보통 그렇게 안좋아함.)

Gain / Phase Margin

$C(s)$와 $G(s)$로 구성되어있는 Feedback system에서, $G(s)$의 input인 $u$의 크기와 phase를 변화시켜 robustness를 확인할 수 있음.

input Gain $k$를 양수 범위 내에서 확장, 축소시켜 $k_{max}, k_{min}$을 찾음. 그것이 Gain margin

eg ) LQR controller, gain margin ; 1/2 to infty

Phase Margin : instead of gain $k$, $e^{-ts}$를 넣어 phase를 변화시키기. (time domain으로 가게 되면 time delay가 됨) :

think of Laplace Transform,

$e^{j\theta} = e^{-jtw} = e^{-Ts}$, $F(u(t))e^{j\theta}\leftrightarrow u(t-T)$

그렇게 했을 때 최대 최소 안정도를 찾음. 이 것이 Phase margin. 당연히도 대칭성이 보장됨. (Nyquist plot이 대칭이므로)

eg) LQR의 phase margin 은 $\pm 60\text{deg}$

감싸지는 횟수의 변화가 없도록 하는 최대 범위가 Gain/Phase margin임

Nyquist plot 관점에서 gain/phase margin은 nyquist plot을 $k$배 확대, 축소시켰을 때 $-1$의 encirclement가 바뀌는지 여부이고, phase의 경우 크기는 유지하고 원점을 기준으로 돌렸을 때를 의미.

Relationship with Nyquist plot and Bode plot

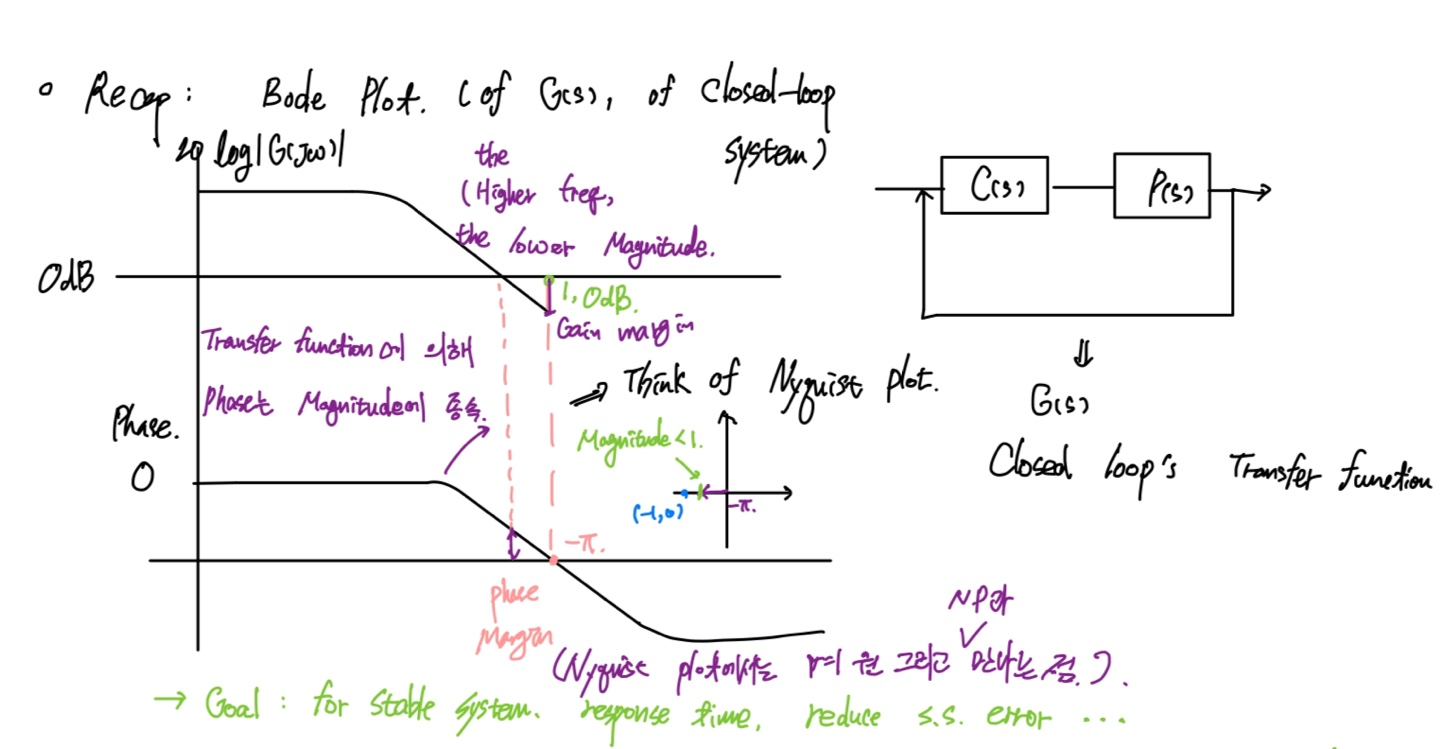
Nyquist plot과 Bode plot은 본질적으로 같은 것을 의미하고 있음.

Bode plot은 w에 따른 $G(jw)$의 phase, magnitude를 표현하고 있는 것이며, Nyquist plot도 해당 정보를 Complex plane에 찍은 것임.

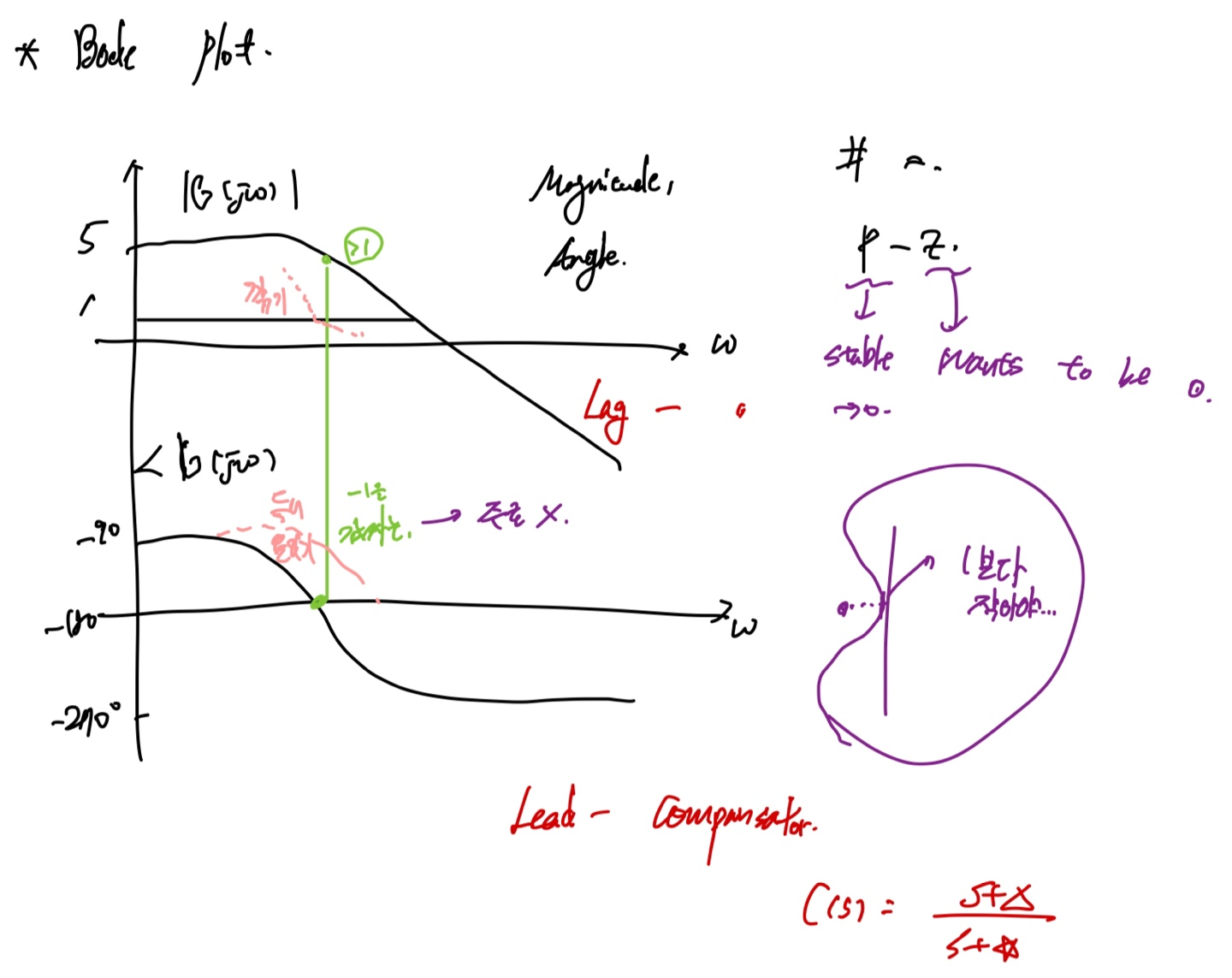
고전 제어에서 (간단한) system의 bode plot은 Magnitude의 경우 low frequency에서 일정하고, high freq에서 깎여나가는 모양이며, Phase는 -90도 ~ -270도 사이를 한번 cross하는 형태로 만들어짐

이 때 Magnitude의 0dB (1)을 지나는 순간 phase가 -180도보다 크거나, 반대로 -180도를 지나는 동안 Magnitude가 1 (0dB)보다 낮아야만 system은 stable하다고 할 수 있다. 한바퀴 도는 Nyquist plot을 생각해보면, -180도에서 크기가 1보다 작아야만 “$-1$”을 enclosement에 포함하지 않을 수 있음.

Bode plot에서 Phase margin / Gain margin을 확인

Phase가 $-\pi$일 때에 대한 $j\omega$에 해당하는 Magnitude가 gain margin

Magnitude가 0dB일 때의 $j\omega$에 해당하는 phase가 phase margin

Lead-Lag compansator

위의 수식에서 알 수 있듯이 Magnitude plot을 조금 깎아서, 혹은 phase plot을 조금 들어올려서 0dB가 되는 지점이 -180도보다 phase가 작아지게 만들어야 함. 이를 위해 새로운 1차 Controller를 도입한 것이 Lead-lag compansator이다.

Magnitude를 줄이는 경우가 Lag compansator,

Phase를 들어올리는 경우가 Lead compansator라고 함

use $C(s) = \frac{s+b}{s+a}$ 사용, or $C(s) = \frac{b}{a}\frac{s/b+1}{s/a+1}$

Lead compansator : $a>b>0$인 경우

Lag compansator : $b>a>0$인 경우.

Lead의 경우 분자가 먼저 들어올려지고 ($b$), 분모에 의해 내려오므로, magnitude는 $b/a$에서 1로 살짝 들어올려짐. Phase의 경우 0도에서 +90도까지 갔다가 다시 0도로 내려와 결과적으로 phase를 들어올리는 효과가 dominant함을 알 수 있다.

Lag의 경우 분모에 의해 먼저 내려가고($a$) 분자에 의해 다시 돌아오므로, magnitude가 $b/a$에서 내려가 -1로 가게 됨을 알 수 있다. phase는 -90도 를 찍고 다시 0도로 돌아오는데, 이 때는 high freq에서 Magnitude를 끌어내리는 효과를 주는 것을 알 수 있음.

1차 t.f로 구성된 Lead-lag compansator는 Passive 소자들(RC, RL circuit, OP-AMP(k gain)) 등을 이용해 만들 수 있음.

Loop gain

Closed loop 전체에 대한 transfer function을 $L(s)$라고 함. $C(s)P(s) = L(s)$

일반적으로 $L(s)$는, low frequency에서는 매우 큰 값을 가지고, high frequency에서는 작은 값을 가지는 것이 좋은데 이는, $G(s) = \frac{L(s)}{1+L(s)}$에서 small frequency를 가지는 경우 $L(s) \rightarrow \infty$로 가게 되면 $G(s) \rightarrow 1$ 이기 때문에 좋은것.

$G(s)$로부터 $L(s)$ 찾기 :

\[\begin{aligned}G(s) &= \frac{L(s)}{1 + L(s)} \\L(s) &= \frac{G(s)}{1 - G(s)}\end{aligned}\]

위의 좋은 $L(s)$의 조건으로부터, $L(s)$에 Integrator가 존재할 경우, 즉 $1/s$가 존재하면 Bode plot 상에서 왼쪽으로 갈 때 계속 위로 치솟으므로, 이것이 좋은 $G(s)$, Closed loop tranfrer function의 조건이라 할 수 있음.

Loop shaping

$C(s)$와 $P(s)$로 구성된 system에서, $C(s)$의 feedback 이전에 계속 제공되는 $r$을 Reference, $P(s)$로 들어가는 $C(s)$의 feedback 출력에 가해지는 것을 disturbance(외란), 출력값 $y$(실제)와 이를 sampling 하면서 필연적으로 들어가게 되는 $n$, noise( $C(s)$에는 $y$를 sampling 하는 과정에서의 noise가 필연적으로 포함된다.)

우리가 목표로 하는 $L(s) = C(s)P(s)$에서 $L(s)$의 Bode plot의 Magnitude plot은 감소하는 형태, 즉 low freq에서 높은 magnitude를, 낮은 freq에서 작은 magnitude를 갖는 것.

출력 $y$값에 reference, disturbance, noise 각각을 입력처럼 간주하여 각각의 Transfer function 형태로 나타내게 되면,

\[Y(s) = \frac{L}{1+L} R(s) + \frac{-L}{1+L}N(s) + \frac{P}{1+L} D(s)\]

이로부터 알 수 있는 사실 : $C(s)$를 키우게 되면, $L(s)$도 $C(s)$가 포함되어 같이 커지므로, Noise에 의한 효과를 줄일수는 없음.

한편, noise, disturbance의 일반적인 특징은, noise는 frequency가 높고, disturbance는 frequency가 작다는 것이다. (예를 들면 바람의 방향이 한번에 바뀌지 않고, two-cart system에서 중력에 의해 생기는 힘 등은 거의 상수에 가까움.)

Methods of Control (고전) - Loop shaping methods?

1. Root Locus (적절한 gain K값이나 그 범위를 Complex plane에서의 pole의 위치를 통해 조절)
2. Lead-lag compansator

\[\frac{s+b}{s+a}\]

1. PID control

\[k_p + k_i \int e(t)dt + k_d \frac{d(e)}{dt}\]

Dominent Pole

For stable system, $j\omega$축에 가까운 nearest pole(s)를 dominent pole이라고 함.

pole placement method에 의해 보통 1~2개의 pole만 dominent pole로 놓고, 나머지 pole들은 모두 좌반평면의 먼 곳으로 보내버림.

이러한 방법으로 많은 시스템들을 1차-2차 시스템으로 근사할 수 있음.

이는, $\dot x = Ax$의 해에 의해서, dominent 하지 않은 pole들은 그렇지 않은 pole보다 더 빨리 0으로 죽어 없어져버리므로 생기는 일.

2nd order system의 분석

Consider following Transfer function

\[\begin{aligned}G(s) &= \frac{w_n^2}{s(s + 2\xi w_n)} \\T(s) &= \frac{G(s)}{1 + G(s)} \\&= \frac{w_n^2}{s^2 + 2\xi w_n s + w_n^2}\end{aligned}\]

입력은 unit step function이라 하자.

\[Y(s) = U(s)T(s)\]

by PFE, $y(t)= \cdots$ 로 풀수 있음.

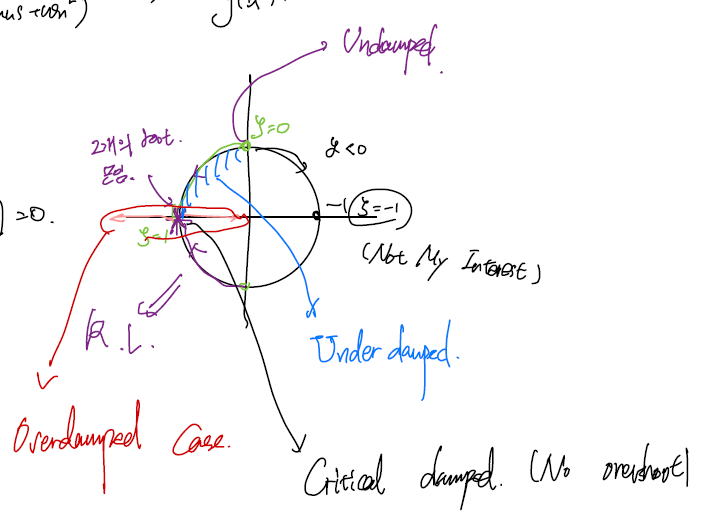
Performing Loot locus on $1+\xi\left(\cdot \right) = 0$

$w_n$을 반지름으로 하는 원 상에서 $\xi=0$에서는 $j\omega$ 축 위에 있다가 점점 미끄러져 내려옴. $\xi=0$ 에서 $-w_n$으로 pole이 모두 모이고, 이후로 좌우로 퍼짐.

2nd order system usf response parameter들

2차 시스템, 혹은 Dominant pole 개념을 이용해서 2nd order system으로 근사되는 시스템들에 unit step function을 인가하였을 때 출력을 parameterization할 수 있음.

• Rise Time ($t_r$) : final value의 10%~90%까지 도달하는데 걸리는 시간
• Peak Time ($t_p$) : 최대 값까지 가는데 걸리는 시간
• Overshoot : 최대값의 최종 값에 대한 % 비율
• Settling time ($t_s$) : 최종 값의 $\pm x\%$ 값 이내로 줄어드는 데까지 걸리는 시간
• Steady state-error : Input step value와 최종 값 과의 차이

다음과 같이 수식적으로도 표현 가능