[제어공학개론] Lec 15 - Classical control

📢Precaution

본 게시글은 서울대학교 심형보 교수님의 23-2 제어공학개론 수업 내용을 바탕으로 작성되었습니다.

Routh-Hurwitz Criterion

Polynomial의 근의 real part가 음수인지, 양수인지 그 여부를 근을 직접 구하지 않고 알아낼 수 있는 방법.

다시 말해 어떤 행렬 $A$가 Hurwitz인지 알 수 있음.

\[\text{consider polynomial : } a_n s^n + a_{n-1}s^{n-1} + \cdots +a_0 = 0\]

Real Part의 부호의 변화를 알 수 있음.

1. polynomial의 계수들을 세로로 번갈아 가며 쓰기.

\[\begin{aligned} a_n && a_{n-2} && a_{n-4} && \cdots && a_1\text{ or } a_0 \\ a_{n-1} && a_{n-3} && a_{n-5} && \cdots && a_0\text{ or blank} \end{aligned}\]

1. 그 다음 줄은, 바로 윗줄의 가장 왼쪽 원소를 분모로 하고, 첫번째 열과 자신의 오른쪽 열에 대해 2x2 matrix의 Determinent처럼 계산을 진행하여 써준다. (단 determinent랑은 부호가 다름.)

\[\begin{aligned} a_n && a_{n-2} && a_{n-4} && \cdots && a_1\text{ or } a_0 \\ a_{n-1} && a_{n-3} && a_{n-5} && \cdots && a_0\text{ or blank} \\ * /a_{n-1} && ** /a_{n-1} && \cdots \end{aligned}\] \[* = a_{n-1} a_{n-2} - a_n a_{n-3}\] \[** = a_{n-1} a_{n-4} - a_n a_{n-5}\]

1. 같은 방법으로 계산을 반복하여 최종적으로 한 행에 하나의 원소만 남을 때 까지 반복함. 삼각형 모양이 되면, 첫번째 열의 array의 부호가 바뀐 횟수를 곧 우반 평면의 근의 횟수로 생각.
   • 예를 들어 부호가 다 —-, 다 ++++인 경우는 Hurwitz임. (부호가 다 안바뀌었으므로, 모든 애들이 좌반평면에 있음.)
   • 반대로 –++– 와 같이 바뀐 경우는 부호가 2번 바뀌었으므로 우반평면에 근이 2개 위치하였다고 볼 수 있음.

Root Locus

G(s)의 전달 함수를 가진 System에 $K$의 미지의 Gain을 주어 Feedback system을 구성. 이 때 어떤 $K$ 값의 범위에서 안정한지를 판단할 수 있는가?

\[T(s)=\frac{kG(s)}{1+kG(s)}\]

$\text{Denominator} = 1+kG(s)$ 의 근의 부호를 Routh-Hurwitz Criterion으로 확인하여 안정성을 check할 수 있음.

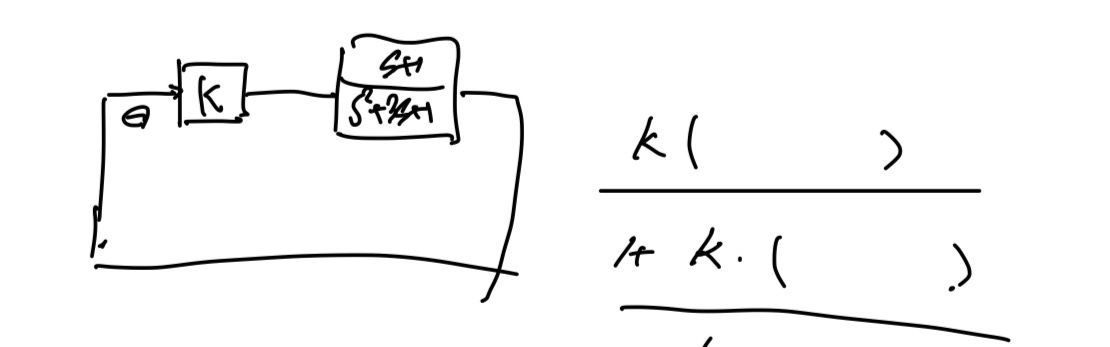
For postive $K$, consider transfer function of closed loop

$k$(gain) 값이 바뀜에 따라 Closed loop의 pole이 어디에 있는가? single parameter $k$가 바뀜에 따라 복소평면에서의 pole의 위치의 궤적을 그린 것.

\[G(s) = \frac{N(s)}{D(s)}\] \[Den(s) = D(s)+kN(s)\]

어차피 $1+kG(s) = 0$을 만들것이므로,

\[\begin{aligned}k G(s) &= -1 \\\vert G(s) \vert &= \frac{1}{k} \\\angle G(s) &= -\pi \pm 2k\pi, \quad k \in \mathbb{Z}\end{aligned}\]

1. Open loop의 Pole, zero에 점을 찍자.
2. Test Point(어떤 점)은 Loot locus 선 위에 올라가있는지를 확인하려면, 각각의 Angle 기여도를 더하는데, zero의 Angle 기여도는 더하고, pole의 Angle 기여도는 빼는 식으로 해서 이 값이 $-\pi + 2k\pi$이어야 함. Test point가 정해졌다는 것은, $s$가 결정되었다는 것인데, $G(s)$에 $s$를 대입하게 되면,

\[\begin{aligned}G(s) &= \frac{(s - z_1)(s - z_2)}{(s - p_1)(s - p_2)(\cdots)} \\\angle G(s) &= (\angle \text{ from zeros}) - (\angle \text{ from poles}) \\&= -\pi + 2p\pi, \quad p \in \mathbb{Z}\end{aligned}\]

k값은 어떤 양수든 될 수 있으니 Angle이 중요.

이러한 식으로 작도법이 존재하는데,

1. $k=0$일 때는 Open loop pole에서 시작할 때 departure angle은 $s$를 조금 변화시켰을 때 나머지에 대한 기여도가 -180도가 되도록 하는 방향으로 출발함.
2. $k$가 무한대로 간다면 $G(s)$가 open loop zero로 감.
   • 너무나 High gain을 쓰게 된 경우, open loop zero로 가게 되는데, 이 open loop zero가 불안정하면 시스템이 불안정해질 수 있다.
   • Open loop zero와 pole의 개수가 서로 다른 경우, 예를 들어, pole이 4개고, zero가 2개인 경우, 나머지 2개는 zero로 가지 않고 무한대로 발산하게 된다. 당연히 $-\infty$로 발산시 가능하나 $\infty$로 발산시 불안정해질 수 있음.

Root locus의 적용,

Root locus는 항상 x축 대칭임. 항상 켤레 근이기 때문.

Root locus는 상수 gain에 대해서만 적용하는 것이 아니라, 관심 있는 단일 parameter를 강제로 root locus 형태로 바꿔주어서 적용이 가능하다.

for example :

\[1+ \frac{s^2 +ks+1}{s^4}\]

$s^4$를 곱해서,

\[\begin{aligned}s^4 + s^2 + ks + 1 &= 0 \\1 + k \frac{s}{s^4 + s^2 + 1} &= 0\end{aligned}\]

로 바꾸어 root locus를 그리면 됨.