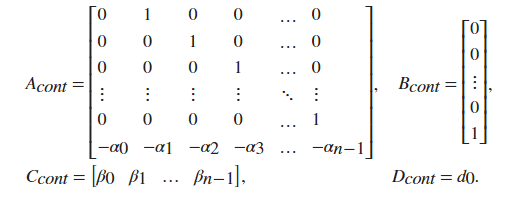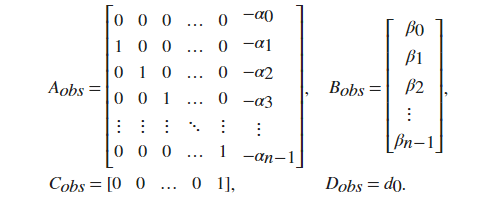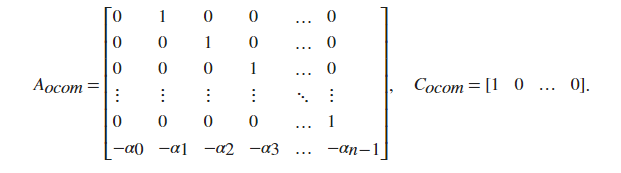[제어공학개론] Lec 09 - Canonical form
제어공학에서 표준형으로 설정된 시스템의 캐노니컬 형식에 대해 설명하며, 제어 가능성과 관측 가능성의 캐노니컬 형식을 수식과 함께 제시합니다. 각 형식은 시스템의 전이 함수를 나타내며, 교과서에 따라 다르게 정의될 수 있습니다.
[제어공학개론] Lec 09 - Canonical form
📢Precaution
본 게시글은 서울대학교 심형보 교수님의 23-2 제어공학개론 수업 내용을 바탕으로 작성되었습니다.
Canonical form
- 수많은 A, B, C, D로 describe 될 수 있는 system을 특정 표준형으로 설정해둔 것.
- 교과서, 참고자료에 따라 다르게 설정할 수 있음.
Controllability canonical form
\[\begin{aligned} A &= \begin{bmatrix}0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ -a_0 & -a_1 & -a_2 & \cdots & -a_{n-1} \end{bmatrix} \\ B &= [0, 0, 0, \cdots, 1]^T \\ C &= [b_0, b_1, b_2, \cdots, b_{n-1}] \\ D &= [D] \end{aligned}\]it represents transfer function
\[T(s) = \frac{b_{n-1}s^{n-1}+\cdots + b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s + a_0}+D\]another book…’s controllability canonical form
- original canonical form
- also called as companion form
Observability canonical form
\[\begin{aligned} A &= \begin{bmatrix}0 & 0 & 0 & \cdots& 0 & -a_0 \\ 1 & 0 & 0 & \cdots & 0 & -a_1 \\ 0 & 1 & 0 & \cdots& 0 & -a_2 \\ \vdots & \vdots & \vdots &\vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots &1 & -a_{n-1} \end{bmatrix} \\ B &= [b_0, b_1, b_2, \cdots, b_{n-1}]^T \\ C &= [0, 0, 0, \cdots, 1] \\ D &= [D] \end{aligned}\]another book…’s observability canonical form
- original canonical form
- companion canonical form
This post is licensed under CC BY 4.0 by the author.