[제어공학개론] Lec 03 - Steady state response, bode plot

📢Precaution

본 게시글은 서울대학교 심형보 교수님의 23-2 제어공학개론 수업 내용을 바탕으로 작성되었습니다.

Stable Transfer function (system)

• P(s)의 모든 pole의 실수부가 음수.
• Consider a differential equation

\[Y(s) = P(s)U(s) = \frac{A}{s-\alpha} + \frac{B}{s-\beta} + \cdots\]

• P. F. E. 를 통해 1차식으로 분해가 되는 것은 결국 $P(s)$나 $U(s)$의 근

\[\Re{\{\alpha, \beta,\cdots\}}<0\] \[Y(s) = Ae^{\alpha t}+ Be^{\beta t}\]

pole의 Real part는 결국 time domain에서의 expotenent에서의 amplitude가 되므로, pole의 실수부가 음수여야지만 시간이 지남에 따라 수렴성이 생김.

즉 Stable Transfer function은 Transfer function의 Pole의 실수부가 모두 음수임.

$Y(s) $ (출력) $= U(s)T(s)$로, 입력의 Laplace transform을 마치 Transfer function과 같이 본다면 출력은 입력의 신호와 Plant의 신호의 합이라고 볼 수 있다.

Steady-state Response to sinusodial Input (steady plant)

suppose… ($u(t) = \sin{\omega t}$)

Steady-state response (정상 상태 response)

• caused by input $u(t)$
• 일정 시간이 지난 후 안정화됨

Transient Response (과도기적 response)

• caused by plant (결국 0으로 수렴하나, 시작 후 잠시동안 존재하는 신호들)

Sin파의 입력을 넣는다면,

\[y_{ss}(t) = |P(jw)| \sin{(\omega t + \angle P(j\omega))}\]

$\omega$의 주파수를 갖는 사인파를 넣는다면, 출력 또한 $\omega$의 주파수를 갖게 됨 : LTI system이기 때문(선형 시불변 시스템)

Transients : $P(s)$의 poles에 의해 생긴 것을 PFE 하는 것이므로, 결국 수렴함.

Proof :

\[\begin{aligned}Y(s) &= P(s)U(s) \\ &= P(s)\frac{\omega}{s^2+\omega^2} = \frac{as+b}{s^2+\omega^2} + \text{ Transients} \end{aligned}\]

Multiplying $(s-j\omega)$ on both sides :

\[\begin{aligned}P(s)\cdot \frac{\omega}{s^2+\omega^2} &= \frac{as+b}{s+j\omega} \\ s=+j\omega& \\ P(j\omega) \frac{\omega}{2j\omega} &= \frac{as+b}{2j\omega} \\ P(j\omega) &= aj +\frac{b}{\omega}\end{aligned}\]

Magnitude & angle :

\[\begin{aligned} |P(j\omega)| &= \sqrt{\bigg(a^2 + \frac{b^2}{\omega^2}\bigg)} \\ \angle P(j\omega) &= \tan^{-1} {\bigg(\frac{b}{a\omega}\bigg)} \end{aligned}\]

To get $y(t)$ :

\[\begin{aligned} y(t) &= \mathcal{L}^{-1}\{\frac{as+b\cdot \omega/\omega}{s^2+\omega^2}\} = a\cos { \omega t} + \frac{b}{\omega} \sin{\omega t} \\ &= |P(j\omega)| \bigg(\sin{\angle P(j\omega) \cos{\omega t} + \cos \angle{P(j\omega) }\sin \omega t}\bigg) \\ &= |P(j\omega)| \sin{\bigg(\omega t + \angle P(j\omega)\bigg)} \end{aligned}\]

For example :

\[\begin{aligned} u(t) &= 2\sin{t} + 3\cos{(2t+1)} \\ T(s) &= \frac{1}{s+1} \end{aligned}\]

signal의 중첩의 경우, Linearity holds.

\[\begin{aligned} |P(j\omega)| &= |\frac{1}{j\omega+1}| \\ \angle P(j\omega) &= \angle \frac{1}{1+j\omega} \\ |P(1\cdot j)| &= |\frac{1}{1+j}| = \frac{1}{\sqrt 2} \\ \angle P(1\cdot j) &= \angle \frac{1}{1+j}= -\frac{\pi}{4} \\ |P(2\cdot j)| &= |\frac{1}{1+2j}| = \frac{1}{\sqrt 5} \\ \angle P(2\cdot j) &= \angle \frac{1}{1+2j}= \theta \end{aligned}\] \[\begin{aligned} y(t) &= 2 |P(j)| \sin(t+\angle P(j)) + 3 |P(2j)|\cos(2t+1+\angle P(2j)) \\ &=\sqrt 2 \sin(t-\frac{\pi}{4}) + \frac{3}{\sqrt 5} \cos (2t+1+\theta) \end{aligned}\]

주파수에 따른 증폭비, Phase angle이 다르며, 이를 Plotting 한 것이 Bode Plot이다.

Steady state Response to arbitary input

Fourier transform을 통해서 function을 sin, cos으로 만들고, 위의 과정을 반복하면 됨.

Input signal u(t)의 푸리에 변환 $u(j\omega)$를 그대로 활용할 수 있음. (물론 scale의 변환은 거쳐야 하지만)

$\left.P(s)\right\vert_{s=j\omega}$ 는 안정하다는 조건이 붙어야만 넣을 수 있음.

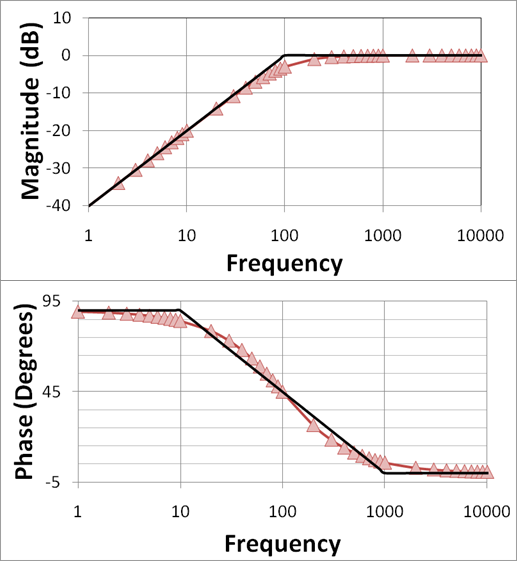
Bode plot

Transfer function의 Amplitude와 Angle을 주파수 $\omega$에 따라 plot한 것.

Amplitude, freq에는 각각 $20\log_{10}$, $\log_{10}$을 씌운 뒤 plot

각각을 Magnitude plot, Phase plot이라고 함.

• log를 씌웠을 때의 장점 : 저주파에 대한 해상력이 높으며, 고주파 대역도 넓은 범위를 한 눈에 볼 수 있음
• log를 씌웠을 떄의 단점 : DC gain을 보기에는 적합하지 않음. (DC gain of the system : input=1은 $\cos 0\cdot t$로 볼 수 있는데, 이 때의 Amplitude는 $\omega=0, \log_{10}\omega =-\infty$이므로, 그래프에 표시되지 않음.)

Reason why $20\log_{10}$

dB : “decibel”

X=1, 0dB / X=10, 20dB / X=$\sqrt 2$ , 3.01dB

즉 dB는 증폭비를 의미함.

20dB 단위로 신호가 10배가 됨.

Bode plotting Rational Transfer function

All polynomials can be expressed in product of 1st, 2nd order polynomials (Real)

for example :

\[P(s) = \frac{(s+z_1)(s+z_2)}{(s+\lambda_1)(s+\lambda_2)^2(s^2+\zeta \omega_n s + \omega_n^2)}\]

전체 $P(s) = P(j\omega)$로 놓고, 식의 양변에 $20\log_{10}$, 절댓값을 취해 주면,

\[\begin{aligned} 20\log_{10}|P(j\omega)| =\ & 20\log|j\omega+z_1| + 20\omega|j\omega + z_2| \\ &- 20\log|j\omega+\lambda_1| - 20\log|j\omega + \lambda_2| \\ &-20\log|(j\omega)^2 + \zeta\omega_n j\omega + \omega_n^2| \end{aligned}\]

First order polynomial

\[20\log|j\omega+z_1|\]

$\omega«z_1$

(given) $\approx20\log z_1$

$\omega\approx z_1$

(given) $\approx20\log \sqrt 2 z_1$

$\omega»z_1$

(given) $\approx20\log \omega$

$\omega$가 작을 때는 $\omega$의 값에 영향을 받지 않는 상수함수.

$\omega$와 $z_1$의 크기가 비슷할 때는 약 $\sqrt 2$만큼 차이가 나게 됨. (상수함수 보다)

$\omega$의 크기가 더 클 때는 기울기가 20 dB/decade인 선형함수가 됨.

20 dB/decade : 10배당 20dB가 차이나는 것. (Bode Amplitude plot에서 20과 동일)

• zero : 해당 값 이후로 무조건 상승
• pole : 해당 값 이후로 무조건 하락

Phase plot의 경우 : 각각의 phase들의 summation으로 이미 이루어져 있으므로, 굳이 log를 취하지 않고 계산해도 됨. (각각의 합)

\[\angle P(j\omega) = \angle (j\omega + z_1) + \angle (j\omega + z_2) + \cdots - \angle(j\omega + \lambda_1) + \cdots\]

Second order polynomial

consider :

\[20\log \vert\frac{\omega_n^2}{(j\omega)^2 + 2\zeta \omega_n s + \omega_n^2}\vert\]

root of $s^2 + 2\zeta \omega_n s + \omega_n^2=0$

\[\begin{aligned} s &= -\zeta \omega_n \pm\omega_n\sqrt{\zeta^2-1} \\ s &= -\zeta \omega_n \pm j\omega_n \sqrt{1-\zeta^2} \end{aligned}\]

$\omega_n$

natural frequency

$\zeta$

Damping ratio (only defined at stable pole, 해가 복소평면상의 2, 3사분면에 존재)

$0<\zeta<1$ : 복소평면에 표시해보면, 양쪽 y축과의 교점이 $\zeta=0$, $\zeta=1$인 지점은 (-1,0)

P(s)에 $j\omega$ 대입시

\[20\log \vert\frac{\omega_n^2}{(\omega_n^2-\omega^2)+j(2\zeta\omega_n))}\vert\]

graph로 그려보았을 때…

$\omega$가 작을 때는 $\omega$의 값에 영향을 받지 않는 상수함수.

$\omega$와 $\omega_n$의 크기가 비슷할 때는 $\zeta$의 값에 따라 natural frequency에서 resonence를 일으키게 됨. 특히 $\zeta$가 0일 경우 발산함. $\zeta = 0.707 = 1/\sqrt 2$인 경우 No peak

$\omega$의 크기가 더 클 때는 기울기가 -40 dB/decade인 선형함수가 됨.

Phase plot의 경우 처음 $+\displaystyle{\pi\over 2}$를 유지하다, $\omega_n$을 기점으로 반전되어 $-\displaystyle{\pi\over 2}$가 됨

why natural frequency ? : impulse($\delta(t)$)를 입력시 natural frequency이 가장 dominant하게 진동하는 모습을 볼 수 있음.

$\zeta=0$이어도 impulse를 넣으면 발산하지는 않음. natural frequency에 맞추어 입력신호를 주면 공진

State-space Representation

consider nth order differential equation :

\[\begin{aligned} y^{(3)}(t) + a_2y^{(2)}(t) + \cdots + a_0 y(t) &= b_0 u(t) \\ x_1(t) &= y(t) \\ x_2(t) &=\dot y(t) \\ x_3(t) &= \ddot y(t) \\ &= -a_0x_1-a_1x_2 -a_2x_3-v_0u(t) \end{aligned}\]

$x_1, x_2, x_3$ : state(상태 변수)

Matrix representation of Differential Equation

matrix representation of D.E. :

\[\begin{aligned} \dot x(t) &= Ax(t)+ Bu(t) \\ y(t) &= Cx(t)+Du(t) \\ A &= \begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ a_0 & a_1 & a_2\end{pmatrix}\\ B &= \begin{bmatrix}0 \\ 0 \\ b_0\end{bmatrix}\\ C &= \begin{bmatrix}1 & 0 & 0\end{bmatrix}\\ D &= [0] \end{aligned}\]

비선형 시스템의 선형화

consider nonlinear system :

\[\dot z(t) = f(z(t), v(t))\]

$v(t)$ is input of the system, $f(z)$ is $(n\times 1)$ vector.

Equibrilium (평형점) :

\[\dot z = f(z) = 0\]

평형상태에선 시간에 따른 변화가 없어야 하므로, 평형점의 $z=z^*$

• 평형점의 유일성은 보장되지 않음.

example )

\[\begin{aligned} \dot z_1 &= z_2 \\ \dot z_2 &= z_1^2 - 1 + \cos{(z_2)} \end{aligned}\] \[\begin{aligned}f(z) &= f(z^*)+ f'(z^*)(z-z^*)+\text{H.O.T} \\ f(z) &= f(z^*) + \frac{\partial f}{\partial x} (z^*)(z-z^*) +\text{H.O.T}\end{aligned}\]

Equibrilium이므로,

\[{\bf f}(z) = {\bf f}(z^)+ \frac{\partial f}{\partial \bf z}(z^)(z-z^*)+\text{H.O.T}\]

H.O.T(Higher order term) : $z-z^*$의 2차 이상 항은 0으로 근사 가능.

$\displaystyle\frac{\partial f}{\partial \bf x}$

Jacobian of f

\[\frac{\partial f}{\partial \bf x} := \begin{bmatrix}\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots &\frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots &\frac{\partial f_2}{\partial x_n}\\ \vdots & \ddots & & \vdots \\\frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots &\frac{\partial f_n}{\partial x_n} \end{bmatrix}\]

$\frac{\partial f}{\partial \bf x}(z^)$ : f의 Jacobian을 계산한 다음, z자리에 $z^$을 대입한 것.

Equibrilium 기준 $f(z^* ) = 0$이며, $\frac{\partial f}{\partial \bf x}$ 은 $(n\times n)$ matrix 이므로 이를 정리하면,

\[f(z) \approx A (z-z^* )\] \[\text{z value near } z^*\]

치환을 통한 $z^* $의 소거

치환을 통해 간단한 선형시스템으로의 Linearlize($\dot x = Ax$)로 전환이 가능.

\[\begin{aligned} \text{let } {\bf x} &= {\bf z} - {\bf z^* } \\ \dot {\bf x} &= \dot z - 0 = A{\bf x} \end{aligned}\]

Input이 있는 경우의 선형화

먼저 입력 $v^{*}$ 이 입력되었다고 가정하고,

$f(z^{}, v^{})=0$을 만족시키는 $z^{}, v^{}$ 을 찾기.

\[\begin{aligned} \text{Find } &z^*, v^* \text{such that } f(z^*, v^*)=0 \\ f(z, v) =& f(z^*, v^*) + \frac{\partial f}{\partial z}(z^*, v^*) (z-z^*) + \\ & \frac{\partial f}{\partial v}(z^*, v^*) (v-v^*) + \text{H.O.T} \\ =& A{\bf x} + B {\bf u} \\ \end{aligned}\] \[A = \frac{\partial f}{\partial z}(z^*, v^*) , B=\frac{\partial f}{\partial v}(z^*, v^*)\]

with the same method, we also can linearlize output of non-linear function

let’s say $w(t) = h(z(t), v(t))$

\[f(z^*, v^*)=0, \ h(z^*, v^*)=:w^* \\\] \[\begin{aligned} w(z, v) =& w(z^*, v^*) + \frac{\partial w}{\partial z}(z^*, v^*) (z-z^*) + \\ &\frac{\partial w}{\partial v}(z^*, v^*) (v-v^*) + \text{H.O.T} \\ \\ y =& w(z,v)-w^*= C{\bf x} + D{\bf u} \end{aligned}\] \[C = \frac{\partial w}{\partial z}(z^*, v^*) , D=\frac{\partial w}{\partial v}(z^*, v^*)\]