[일반화학] Lec 10 - Solubility

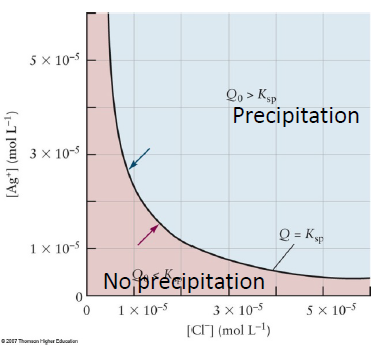
용해도곱 상수(이온성 결정 )

• Gram Solubility, Molar Solubility : 1L의 물에 용해되는 그램수, 몰수
• 용해 반응에 대한 평형상수를 통해서 녹는 몰농도를 계산할 수 있음 → $\Delta G$를 이용하여 경향성 파악

\[AgCl(s) \leftrightarrow Ag^+(aq) + Cl^-(aq)\]

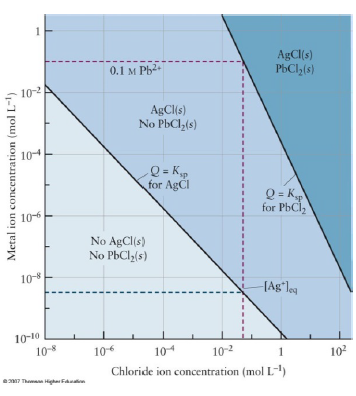
용해도 차를 이용한 분리

• 용해도곱 차이가 나므로, $Ag$를 모두 침전시키고 $Pb$만을 남길 수 있을 것으로 예상. 이 때 넣어야 할 $Cl$은?
• $Pb$가 녹아있을 수 있는 최댓값만큼 넣음. 이에대한 계산 :

\[Q = \lbrack Pb^{2+}\rbrack\lbrack Cl^-\rbrack^2 <K_{sp} = 2.4\times 10^-4\]

• $\lbrack Cl^- \rbrack  = 0.049M$
• 이 때의 Ag의 농도는 Cl의 농도에서 아래로 쭉 내려서 확인가능. 매우 작음 → 대부분 용출됨

농도와 용해도의 관계

• 완충용액 : pH, pOH가 일정하다고 간주,

\[Zn(OH)_2 \leftrightarrow Zn^{2+}+2OH^-\]

• OH-가 고정됨, 물에 녹을 땐 잘 녹지 않지만, 산성 용액일 때는 OH의 농도가 낮음, 용해도 상승
• 용해된 이온이 약산의 짝염기라면 → 산의 추가 → 용해도의 상승
• $CaF_2(s) \leftrightarrow Ca^{2+}+2F^-$ 에서, $H^++F^- \leftrightarrow HF$의 K=1/Ka »1
• $CaCl_2$에서는 안생기는 이유 : Cl-가 강산인 HCl의 짝염기기 때문

배위 화합물에서의 용해도곱상수

\[AgBr \leftrightarrow Ag^+ + Br^-\]

• Ksp 매우 낮으나,
• $Ag^+ + NH_3 \leftrightarrow Ag(NH_3)^+, Ag(NH_3)^+ \leftrightarrow Ag(NH_3)_2^+$ 반응 K가 매우 커 용해 잘시킴
• 물 분자와의 반응하는 경우 존재