[일반화학] Lec 09 - Acid, Base

산, 염기의 정의

• Arrhenius definition : H+, OH-
• Bronsted-Lowry : proton donor, proton acceptor
• Lewis definition : electron pair acceptor,. electron pair donor (BF3, NH3 등을 설명할 수 있음) (전자쌍 : 산화수가 변화하지 않음)

전자가 전달되는 반응

• 산화 환원 반응 (전자 전달, 산화수 바뀜)
• 산-염기 반응 (전자 전달, 산화수 바뀌지 않음)

산화물 (Acidic, Basic and Amphotheric Oxides) (물과의 반응)

• 산소와 비금속 : 주로 산성
• 산소와 금속 : 주로 염기성
• 산소와 준금속 : 산성과 염기성을 모두 가짐(Al, Sn, Zn)

물의 자동 이온화

• 25도에서 K =10^-14, 온도 올라갈 떄마다 K 올라감.
• 비 : 산성, NOx → 미세먼지, 물에 녹았을 때 산성

강, 약 산/염기

• 강산, 강염기 : 녹은 만큼 수용액이 되고 H+나 OH-로 분리됨. (넣은 만큼)

\[K = K_a = {[H_3O^+][A^-]\over [HA]}\] \[pK_a = -logK_a\]

• 강산의 짝염기는 약함, 강염기의 짝산은 약함. ..
• 짝산-짝염기 관계의 두 K 값을 곱하면 $\lbrack H_3O^+\rbrack\lbrack OH^-\rbrack$가 됨. (강산은 제외)
• 강산은 모두 녹는다.

분자 구조와 산의 세기

• 수소로부터 공유전자쌍을 잘 떼어낼 수록 산의 세기가 강해짐.
• HF, HCl, HBr, HI : HF는 너무 작아서 예외, 전기음성도 순
• $CH_4, NH_3, H_2O, HF$ : F, O, N, C 순으로.
• HClO, HBrO, HIO : Cl > Br > I
• $HClO, HClO_2, HClO_3, HClO_4$ : 산소가 많을 수록 잘 당김
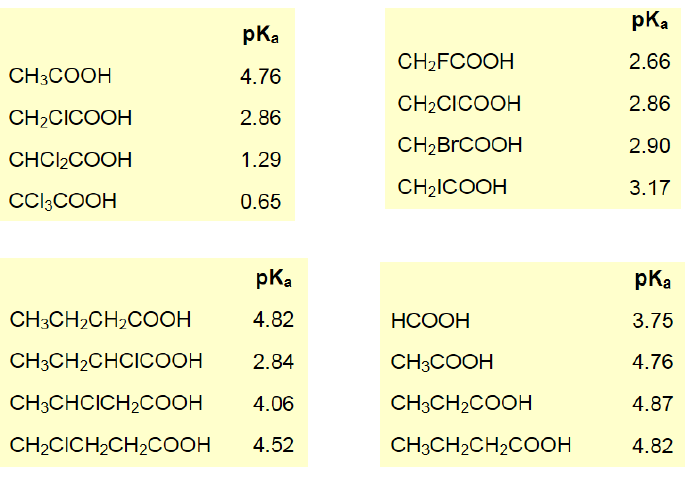
• 카복실기의 예시도 동일

• 단, $CH_3$의 경우 전자 밀어내는 경향

지시약

• 지시약도 아주 약산, 약 염기 경향을 가지고 있음
• 연결된 이중 결합 : 가시광선 영역으로 발광
• 지시약의 색 변화 : $pK_{In}$ 주위에서 그 색의 변화가 일어남

\[K_{In} = K_a = {\lbrack H_3O^+\rbrack \lbrack In^-\rbrack \over [HIn]}\]

• 개중에는 색 변화가 여러번 일어날 수도 있음.

염(Salt) 의 액성

양이온 :

• 산성염 : 약염기의 짝산($NH_4, C_6H_5NH _3^+$ 등) or 작고 +전하가 큰 금속양이온 $(Fe^{3+}, Cu^{+})$
• 중성염 : 약염기의 짝산이나 +전하 있는 금속 양이온 중 1가 이온 ($Li^+, Mg^{2+}, Ag^+$)
• 염기성염 : 없음

음이온 :

• 산성염 : 매우 적음 ($HSO_4^-, H_2PO_4^-$)
• 중성염 : 강산의 짝염기 ($Cl^-, ClO_4^-, NO_3^-$)
• 염기성염 : 약산의 짝염기 ($CH_3COO^-, F^-, S^{2-}$)

강산의 이온화 (매우 옅은)

• 물의 자동이온화를 고려해야 함. 식 3개 (물의 자동이온화, $\lbrack A^-\rbrack $의 농도는 기존에 넣은 강산의 농도와 같음, charge balance)

\[\lbrack H_3O^+\rbrack = \lbrack OH^-\rbrack +\lbrack A^-\rbrack\]

다양성자산

• 무조건 첫번째 H를 떨어트리는게 가장 쉽고, 그 이후는 점점 어려워짐. (pKa 점점 커짐)
• 일반적으로 Ka1만을 고려
• 또한, Ka2의 역반응에 대한 $K_b={K_w\over k_{a2}}$ 와, Ka1의 값이 모두 염의 초기농도보다 작다면

\[pH = {1\over 2}(pK_{a1}+pK_{a2})\]

Buffer (완충 용액)

• 약산이나 약염기의 짝산과 그 짝염기를 넣어서 용액을 만들면 완충 용액이 됨
• 계산 시에 변화하는 x의 양을 매우 작다고 근사할 수 있음 (이 것이 헨더슨-하셀바흐 식)

\[pH = pK_a+log({\lbrack A^-\rbrack\over \lbrack HA\rbrack })\]

강산, 강염기의 적정

• 각각의 H+와 OH-를 계산 한 다음 빼 주기. 이후 농도를 (부피 추가되었으므로) 계산하고 pH구함
• 당량점에서의 pH=7, 이는 강산과 강염기의 그 짝염기와 짝산이 약하기 때문.

약산과 강염기, 약염기와 강산의 적정

• 약염기의 전체 몰수 구하기 / 강산이 녹는 몰수 구하기 (안주어졌으면 약염기 양 만큼)
• 남은 약염기 고려해서 그 약염기의 짝산의 몰수, 몰농도 구하기 (더해진 부피만큼 분모 추가)
• 짝산의 가수분해반응에 대한 Ka를 주어진 Kb를 Kw에 나누어서 구함, 이후 계산.
• pH를 -log 해서 구하기
• 반당량점에서는 H-H 식 적용가능, 당량점에서는 강한 쪽의 pH를 따라가는 경향.