[일반화학] Lec 07 - Physical Equilibrium

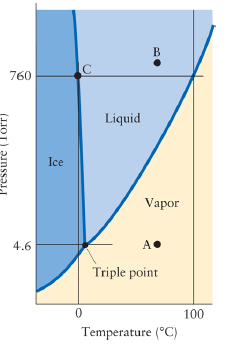
phase diagram

• T, P axis 위에서

특정 P에서의 Gibbs free energy

\[G(P) = G^0 + RTln({P\over P_0})\]

• Solid, V(p)=const, G naught + V(pf-pi)로 표현

Clapeyron equation

• $dG = −SdT + VdP$ 로부터, alpha, beta라는 서로 다른 상의 경계에서의 식은

\[{dp\over dT} = {\Delta_{trans} S \over \Delta_{trans} V}\]

증기압 (vapor pressure)

\[\Delta G_{vap} = G_{gas}-G_{liq} = G_{gas}^0 +RTln({P\over P_0})-G_{liq}^0\]

• at equibrilium, ΔG = 0

\[\Delta G_{vap}^0 = -RTln({P\over P_0})\] \[\Delta G_{vap} = \Delta H_{vap} - T\Delta S_{vap}\]

• naught : 1atm이므로 T1, P1 → T2, P2로 바뀔 때

\[ln({P_2 \over P_1}) = (-{\Delta H_{vap}\over RT_2}+{\Delta S_{vap}^0 \over R})-(-{\Delta H_{vap}\over RT_1}+{\Delta S_{vap}^0 \over R})=-{\Delta H_{vap}\over R}({1\over T_2}-{1\over T_1})\]

• Vaporization : Molecular structure, Temperature에는 영향 받으나 Amount에는 Independent

Volatility and Intermolecular Forces

• High Vap pressure : low intermolecular forces
• e.g. 에탄올(O-H 수소결합) vs 디에틸 에테르 → 에탄올이 증기압 낮음. (결합 강함)

물에서의 solid-liquid boundary, negative slope

• by Clapeyron equation, ΔV < 0이므로 기울기가 아주 살짝 음으로 감

Solubility

• polar-polar끼리, nonpolar-nonpolar끼리 잘 녹음. → 중요한 Factor : Hydrogen Bonding
• polar - nonpolar 결합에서, nonpolar는 결합하는게 좋음 (induced dipole에 의해 결합 좋음) but, polar-polar 결합 끊고 polar-nonpolar결합 하는 것이 polar 입장에서 좋지 않음.
• nonpolar-nonpolar : 엔트로피증가에 의한 효과.

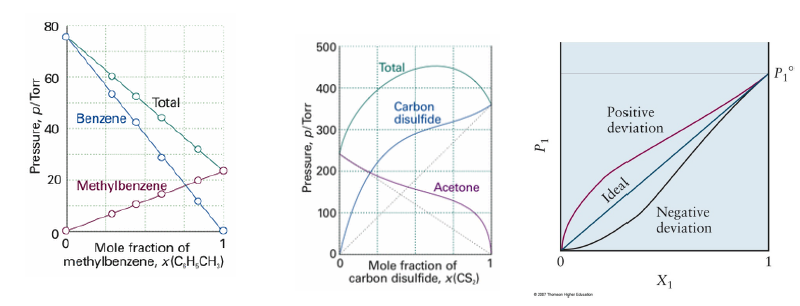
Raults Law for volatile A and B

• 돌턴의 분압법칙에 의해,

\[P_{TOT} = \chi_A P_{A}+\chi_B P_{B} = \chi_A P_{A}+(1-\chi_A) P_{B}\]

Henry’s Law of Solute

• B의 농도가 매우 낮다면, 몰분율에는 still proportional, but pure vapor pressure가 아닌 henry const에 비례함.

\[P_B = {n_B\over n_A+n_B} k_B=\chi_B k_B\]