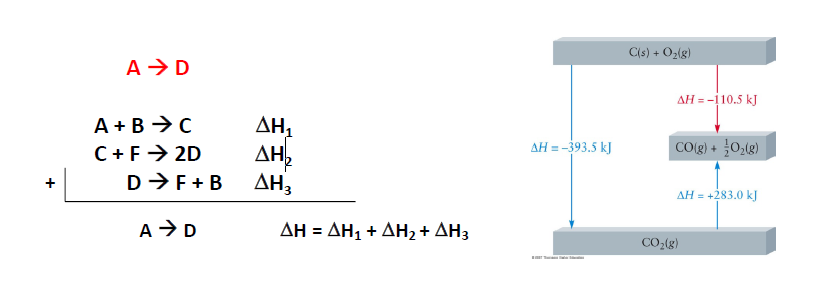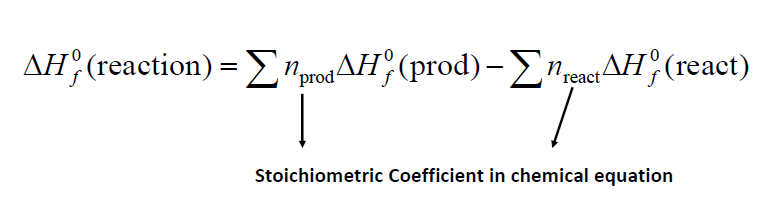[일반화학] Lec 06 - Thermodynamics

열역학

• 반응, 물리적 변화의 방향을 예측할 수 있음.
• 가장 안정한 상을 구할 수 있음.

Psycial meaning of temperature

\[T = ({2\over 3R}) (KE)\]

• 온도가 높으면 높을 수록 에너지가 큼.
• 온도 : Random kinetic energy의 한가지 측정방식

계, 주위

• System : 관심이 있는 대상
• Surrounding : System 주위를 감싸고 있는 ..
• Universe : System + Surrounding
• System의 종류 : Closed, Open, Isolated. (열린, 닫힌, 고립계)

Extensive/Intensive Property

• Extensive : volume, mass, energy
• Intensive : density, pressure, temperature ..

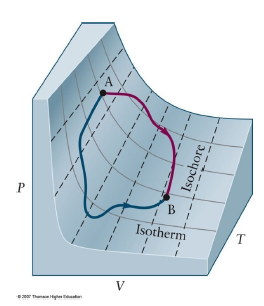
Thermodynamic state : a set of p, V, T, n

• PV=nRT에서 R을 제외한 4개의 변수가 기본 set.

• pv=nrt 공식은 pvt surface를 만듬.
• 해당 상태가 시간에 따라 변하지 않음 - 평형 , Equibrilium
• Reversible process : PVT surface 위에서 현상이 일어남
• Irreversible process : PVT surface를 벗어남.

Energy, Temp, Work and Heat

1. Work :
   • Work = ∫F ⋅ dl
   • 일을 하다 : 나의 에너지를 사용하여 외부에 에너지 공급
   • 일을 받다 : 외부 에너지를 이용하여 계에 에너지 공급됨
   • l, 즉 경로에 관련되있는 함수이므로 Path Funution : 경로함수
   • Work done on the expanding gas : $w= - Ah$
   • 외부 압력에 대해 일을 한 것. (일을 따질 때 마찰력에 의한 일을 일이라고 하는 것 과 같은 이치)
   • Reversible : $P_{int} = P_{ext}$
   • Irreversible : $P_{int} \neq P_{ext}$
   • 전체 Path에 대해 매순간 equibrilium을 유지해야만 reversible work라고 할 수 있음.
2. Temperature
   • Ideal gas에 대해 KE = 3/2 RT
3. Heat : Q
   • 열의 방향성을 결정하는 것은 온도.
   • $C_m$ : molar heat capacity - 몰비열
   • C : specific heat capacity - 비열
   • 온도가 다른 두 물체를 접합하면 온도가 같아질 때까지 열이 이동.

Work & Heat

• Heat : Random motion의 정도.
• Work : 방향성이 있는 motion
• 일 → 열은 쉽지만 열→일은 쉽지 않음.

State function vs Path function

• Path function : 반응의 Path에 dependent ex) Work, Heat
• State Function : 반응의 초기, 나중상태에만 dependent. ex) Total Internal Energy U, Height difference between two point
• Total Internal Energy U 를 구하는 것은 사실상 거의 불가능.

First Law of Thermodynamics

• $U = q + w $ : 계의 내부에너지 변화를 의미.

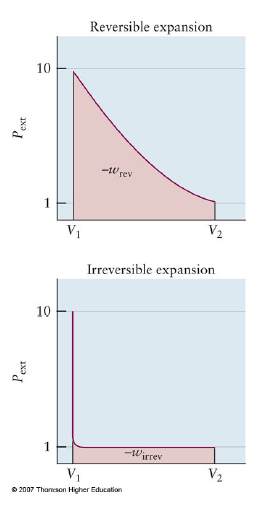
Reversible Isothermal Process of Ideal gas

• Constant T의 경우에 해당
• 가역, 등온압축 or 팽창인 경우.
• 가역이므로 PV=nRT를 만족시키면서 반응이 일어나야 함.

\[w = - \int p_{ext}dV = -\int pdV = -\int {nRT\over V}dV = -nRT ln({V_{f}\over V_{i}})\]

For gas expansion

• $\vert w\vert_{rev} > \vert w\vert_{irrev}$
• Making Engine: 최대한 Reversible하게 함. Carnot engine

Heat capacities of (mono-atomic) ideal gas

• $q_v = nC_v \Delta T$
• Volume change = 0 → w = 0
• $\Delta U_{sys} = w_{sys}+q_{sys} = q_{sys}$
• (일원자분자) $U_{sys} = {3\over 2}nRT,\Delta U_{sys} = {3\over 2}nR\Delta T = q_{sys}$
• $C_v = {3\over 2} R$
• $q_p = nC_p \Delta T$
• $\Delta U_{sys} = w_{sys}+q_{sys} = -P_{ext}\Delta V +q_{sys}$
• (일원자분자) $q_{sys} = {3\over 2}nR \Delta V = {5\over 2}nR \Delta T$ (Constant pressure condition)
• $C_p = {5\over 2}R$
• For Ideal gas (mono-atomic or diatomic) : $C_p − C_v = R$

분자의 형태에 따른 Cv의 차이

• Monoatomic : 3/2 RT
• Linear : 3/2 RT + RT
• non-linear : 3/2 RT + 3/2 RT

Adiabatic Reversible process (q=0) , Isolated system

\[dU_{sys} = nC_v dT = -pdV\] \[T^{C_v\over R} V = const\] \[PV^{5/3} = const\]

• 단열이라고 볼 수도 있지만, 외부에서 열이 들어오기 전에 빠르게 팽창하여 온도가 낮다고 볼 수 있음
• 등온, 즉 PV=const보다 부피 팽창률이 더 작음.

Enthalpy

• 대부분의 화학반응은 등압(1atm) 에서 일어나게 되므로, 팽창하는데 에너지가 사용되고, 나머지는 q, 온도를 올리는데 사용됨.
• 이를 계산하기 편한 State function이 필요하므로 H라는 새로운 변수 만듬.
• $H = U + P ⋅ V$ : state function.
• 등압에서는 P의 변화가 없으므로, $ΔH = ΔU + PΔV $로부터 $q_p = ΔH = nC_pΔT$ 라는 의미를 가지게 됨.
• 즉 등압, Reversible 에서 $ΔH = q_p$ 이므로 열 또한 state function이 될 수 있음.
• Solids에서는 $U = H$ 라고 할 수 있음. (내부에너지 변화에 비해 PV의 변화가 매우 작음)
• 엔탈피가 정의되기 위하여 $W=PV$의 형태로만 일어남, Pext=const, 역학적 평형상태(내외부 압력이 같다) 는 전제가 있어야만 함.

Hess’s Law

• 엔탈피는 상태함수이다. 해당 반응 전후에 일어나는 열 변화를 보려면 과정에 해당하는 반응들의 엔탈피를 계수를 곱하여 합하면 됨.

  

• ΔH > 0, 열을 흡수. ΔH < 0, 열을 방출

ΔH 의 표준화

• Standard state of Matter

  1atm, 특정 T, solution의 경우 1mol/L (1M)

• 해당 상태일 때 naught을 붙일 수 있음.
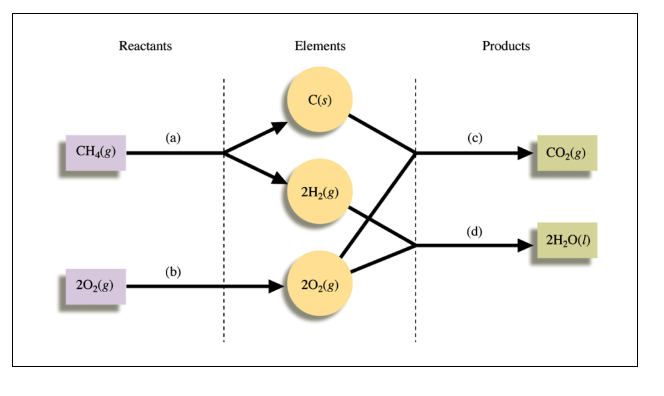
• formation의 경우, 순수한 홑원소 물질에 대해 formation Enthalpy를 0으로 정의함.

• 전체 반응에서의 생성엔탈피는 그 반응물을 홑원소로 분리했다가 다시 생성물로 만드는 반응이기 때문에 prod - react 를 이용

• 엔탈피 : $H=U+PV$ , 일정한 외부 압력에서 반응이 진행되면,

  $\Delta H = \Delta(U+PV)= \Delta U +P\Delta V = q+w+P\Delta V$ $=q-P_{ext} \Delta V + P \Delta V q + (P_{ext}-P) \Delta V $

• 역학적으로 평형상태에 이르렀다면, $P = P_{ext}, ΔHsys = q$

Spontaneous Change (자발성), 엔트로피 (S)

• 엔탈피 변화로는 반응의 자발성을 설명해주지 못함.
• System은 microscopically 가장 probable 한 상태를 취하려 함
• $S_{sys} = k_B lnW$ , Statistical Definiton of Entropy
• W : 가능한 경우의 수, 열역학적으로 randomness 나타냄.
• 열역학적 엔트로피의 정의 :

\[\Delta S_{sys} = {q_{sys,rev}\over T}\]

• Reversible Heat여야만 함. - 실제 반응이 irreversible 이어도 reversible한 경로를 선택
• 주위(Surr) 의 엔트로피를 구할 때는 실제 경로(irreversible) 이용.
• 전체(Universe)의 엔트로피 : reverisble할 때의 univ의 Entropy 동일, irreversible : univ의 Entropy 증가. ($\vert q_{rev}\vert > \vert q_{irr}\vert$)
• Surrounding Entropy :

\[\Delta S_{surr} = {-q_{surr}\over T}\]

• $q_{surr} = q_{sys} $ sys : 가역이라는 조건은 없음.
• 계의 엔트로피 변화는 가역이든 비가역이든 가역경로에 대한 q를 쓰므로 동일 / 주위의 엔트로피 변화는 반응경로에 따라 달라짐

Reversible Isothermal Expansion

\[\Delta S_{sys}=\int_{V_i}^{V_f} {dq_{sys, rev} \over T} = {1\over T}\int_{V_i}^{V_f} dq_{sys, rev} =nRln({V_f\over V_i})\] \[\Delta S_{surr} = -nRln({V_f\over V_i})\] \[\Delta S_{tot} = 0\]

Irriversible Isothermal Expansion

\[\Delta S_{sys}=nRln({V_f\over V_i})\] \[\Delta S_{surr} =\int _{V_i}^{V_f}{dq_{sur, irrev}\over T} = {-w_{surr, irrev}\over T} ={w_{sys, irrev}\over T} ={-P_{ext} \Delta V\over T}=0\] \[\Delta S_{tot} = nRln({V_f\over V_i})>0\]

Reversible Entropy change in Changing T

\[dq_{sys,rev} = nC_{v, p}dT\] \[\Delta S_{sys} = n\int {T_i}^{T_f} {C{v, p}dT\over T} = nC_{v, p}ln({T_f \over T_i})\]

Clausius inequality

\[-w_{sys, rev}>-w_{sys, irrev}\]

• 내가 주위에 일을 해줌 → -값 증가 → 절댓값으로 크기 증가
• 등온이 아니어도 상관은 없지만, 이 때 준 열만큼 일을 하기 때문에 $q_{sys,rev}>q_{sys,irrev}$를 만족함.
• $ΔS_{sys}$의 정의에 의해

\[\Delta S_{sys}={q_{sys,rev}\over T} > {q_{sys, irrev}\over T} ={q_{sys}\over T}\] \[\Delta S_{sys}\geq {q_{sys}\over T}\]

3rd law of thermodynamics

• Nernst heat theorem (experimental observation) : Sulfur(alpha) → Sulfur(beta)의 변환에 대한 엔트로피 변화가 T가 감소할 수록 0에 수렴함.
• Perfect Crystal에서 0K에서의 Entropy=0

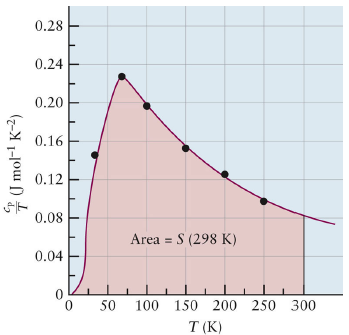
Standard State Entropy values, S naught

\[\Delta S_{rxn}^0 = \sum n_p S_{prod}^0 - \sum n_r S_{react}^0\]

• 특정 T에서 어떤 물질의 엔트로피 구하기

  

\[\Delta S_{sys} = n \int _{T_i}^{T_f} {C_p (T)dT\over T}\] \[S_{sys}(T) = n \int _{0}^T {C_p (T)dT\over T}\]

Carnot 기관의 열 효율 (최대 효율)

\[\Delta S_{univ} = \Delta S_{sys} + \Delta S_{surr} = \Delta S_{sys} + {-|q|\over T_h} \geq {|q|\over T_c}| + {-|q|\over T_h} = |q|({T_h-T_c\over T_cT_h})\geq 0\]

• Heat이 온도 높은 곳에서 낮은 곳으로 이동하는 것은 Spontaneous Process

\[|qc| = |qh| − |w|\] \[\Delta S_{univ} = \Delta S_{sys} + \Delta S_{surr} = \Delta S_{sys} + {|q_c|\over T_c} = |q_{h, rev}|({T_h-T_c\over T_cT_h})-{|w_{rev}|\over T_c}=0\] \[|w_{rev}| = |w_{max}| = |q_{h, rev}|({T_h-T_c\over T_h})\]

• efficiency : $1-{T_c\over T_h}$

Gibbs Free Energy

• 전체 엔트로피를 system에 대한 표현으로 쓸 수 있음

\[\Delta S_{univ} = \Delta S_{sys}+\Delta S_{surr} = \Delta S_{sys}-{\Delta H_{sys}\over T} = -{(\Delta H_{sys}-T\Delta S_{sys})\over T}\]

• at constant T, P
• Gibbs Free Energy : $G_{sys} = G = H_{sys} − TS_{sys}$
• Const T, P에서 $\Delta S_{univ} = -{\Delta G_{sys}\over T}$ 이므로, G의 부호에 따라 자발성 결정
• Standard molar Free Energy Change : $\Delta G^0 = \Delta H^0 - T\Delta S^0$이며 엔탈피와 같은 방법으로 계산

Free Energy and Pressure (평형상수의 결정)

• $G = G^0 +RTln({P\over P^0})$ (for not standard state)

\[dg = dH-TdS = d(U+PV)-TdS = dW+pdV+Vdp-dq = Vdp\] \[\Delta G_{reaction} = \Delta G_{rxn}^0 + RTln({(P_c)^c (P_d)^d\over (P_a)^a (P_b)^b}) = \Delta G_{rxn}^0 + RTln(Q)\]

• Q = K, ΔGrxn = 0 이므로, $lnK = (-{\Delta G_{rxn}^0\over RT})$

Delta G and Nonexpansion Work

• Reversible change, const T, P 에서 $ΔG = w_{extra,max}$ 이므로, 깁스 프리 에너지 만큼 Nonexpansion work를 최대로 할 수 있음

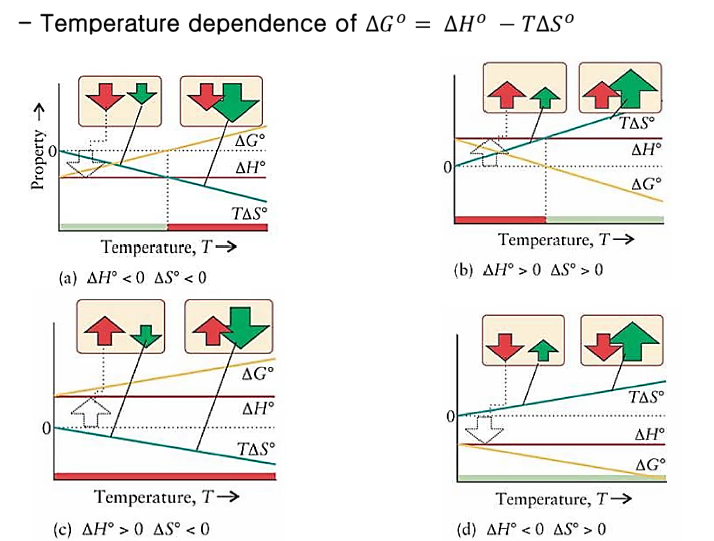
The Effect of Temp.

• H>0, S>0 : 온도 올라감에 따라 자발
• H<0, S<0 : 온도 내려감에 따라 자발
• H<0, S>0 : 항상 자발
• H>0, S<0 : 항상 비자발