[일반화학] Lec 04 - Ideal Gas Law

Gas

1. Pressure
   • Definition of pressure : $P={F\over A}$ 단위 : Newton/m^2 = Pascal
   • 대기압 (Pressure from Atmosphere) =760mmHg at sea level : weight of air
   • $ P= g h$
   • $10^5$Pa = 1bar
   • 1.01325bar = 1atm
2. Temperature
   • Random kinetic energy of molecules

Ideal gas Law

• PV = nRT
• $R=8.314 JK^{-1}mol^{-1}=0.082atm*lK^{-1}mol^{-1}$

Charles’ Law

• At constant Pressure : 기체의 부피는 온도에 비례
• 모든 기체의 부피는 -273.15도에서 0이다.

STP(Standard Temperature and Pressure)

• 273K, 1atm에서 모든 기체 1mol의 부피는 22.4L로 일정
• SATP (Standard Ambient Temperature and pressure) : 298.15K(25도), 1bar 상태

Partial Pressure and Dalton’s Law

• 몰분율 $x_A, x_B$ 가 주어졌을 때 해당 기체의 압력 $P_A = x_A × P$

• Dalton’s Law : Partial pressures of mixture of ideal gas are additive.

  $P = P_A + P_B$ , 전체 압력은 각각의 부분압의 합이다

How to Derive PV=nRT?

• $PV=nRT$ 를 증명하기 위한 몇가지 가정(assumption)
  1. Size of molecule is negligible (분자의 크기는 매우 작음)
  2. Gas molecules are constantly moving in random direction with a distribution of speed (랜덤방향)
  3. Move strait line until it hits the walls (충돌전까지는 직진함)
  4. Elastic (탄성충돌)

Physical meaning of temperature

\[T = ({2\over 3R}) (K.E)\]

• RMS : 위 식을 u 에 대해서 정리해주면,

\[u_{rms} = \sqrt{3RT\over M }\]

Maxwell-Boltzmann distribution:

• 특정 온도에서 기체 분자들은 속도의 특정한 분포를 가지게 됨.

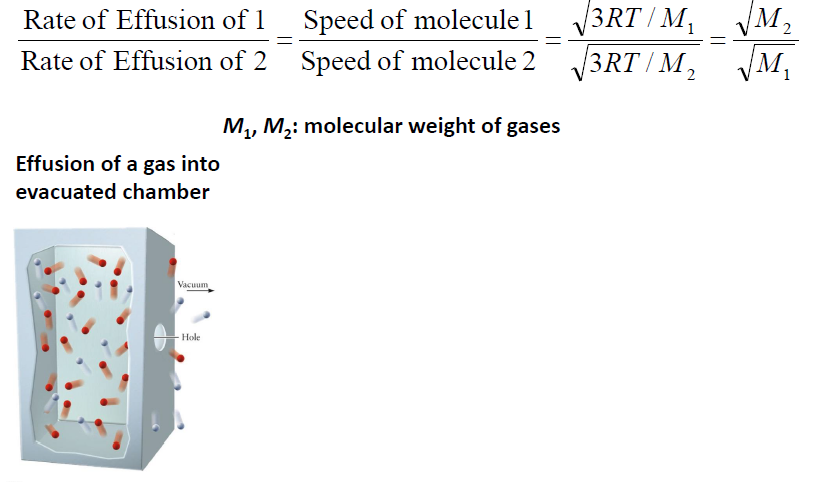
Effusion (기체 분자의 용출, 진공으로부터)

• Graham’s Law of effusion : 서로다른 두 gas가 용출될 때 그 비율은 분자량이 제곱근의 비를 따름.

  

Real, non ideal gases

• PV=nRT는 2가지 가정(분자 자체크기 무시, 서로 상호작용 안함)에 의해 만들어진 공식이므로 이를 고려하게 되면 보정을 해주어야 함.
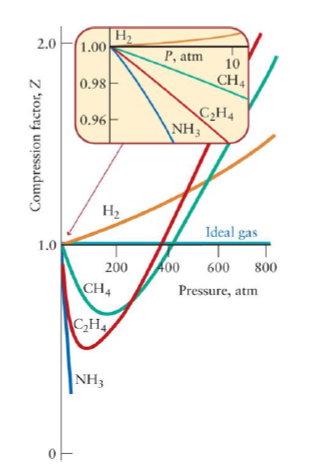
• Compression Factor

\[Z = {PV\over nRT}\]

• Z>1이다 : 동일 P, T 조건에서 V가 PV=nRT의 값보다 더 크게 나옴

• Z<1이다 : 동일 P, T 조건에서 V가 PV=nRT의 갑보다 더 작게 나옴

  

• 압력이 높아질 수록 Z는 달라짐. P가 높아질 수록 분자간의 힘, 분자 자체의 크기를 무시할 수 없게 되므로

Volume Correction

• Free volume 만을 V에 넣어야 함. 즉 실제 측정되는 Volume은 Free volume이 아닌 용기의 volume이므로, 분자의 몰수에 비례, b라는 상수를 곱하여 이를 용기의 volume에서 빼주어야지 free volume이 나옴. 즉 $ V V-nb$ 로 바꾸어 주어야 함.

Pressure Correction

• 분자가 벽을 때리는 단위 면적당 힘이 Pressure인데, 분자가 많이 있으면 그 상호작용에 의해 간섭당하게 됨. 즉 보정이 필요

\[P \rightarrow P + a(n/V)^2\]

• $(n/V)^2$인 이유 : 두 particle 간의 간섭만 생각할 경우 단위 부피 안에 N = n/V 개의 분자가 존재하며, 이들간의 상호작용의 가짓수는 $_{N_0}C_2$이며, 이를 근사하면 위 식을 얻을 수 있음.

Van deer Waals Equation

\[[P_{obs}+a(n/V)^2] \times (V-nb)=nRT\]

• a : 극성 분자, 분자간의 인력이 큰 물질일 수록 큰 경향
• b : 분자의 크기자체가 큰 분자 (크기가 큰 원자가 달린) 일 수록 큰 경향