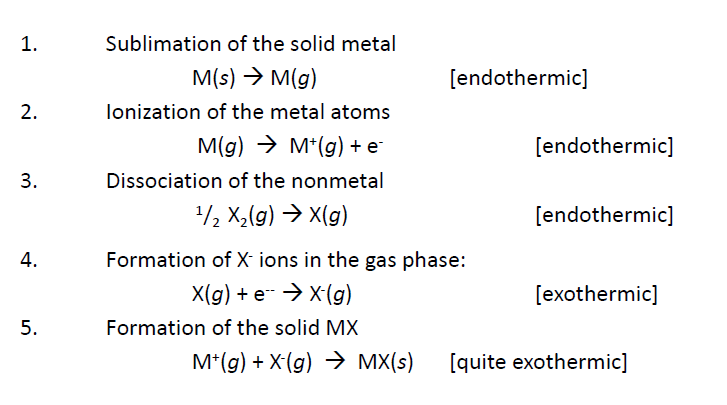[일반화학] Lec 03 - Bonding

이온결합과 공유결합

• Bond length : 옹스트롱 ($10^{−10}m$) 단위를 사용
• 결합의 종류 : 이온결합과 공유결합, 두 원자간의 전기음성도 차이가 클 경우 이온결합, 그렇지 않으면 공유결합.
• 전기음성도(electronegativity) ≠ 전자친화도(electron affinity)
• 전자친화도는 해당 원자가 전자를 하나 받았을 때의 에너지를 의미, unit 존재, 전기음성도는 결합에서 전자를 얼마나 끌어당기는지를 의미, unit 없음
• 전기음성도의 정의 : F가 가장 크므로 이를 4.0으로 정의

Ionic Bonding

• 전기음성도 차이가 너무 크기 때문에 전자를 - 전하쪽이 다 가져갔다고 보고 Coulomb’s Law 적용가능
• $ V(R) = {(Q_1e)(Q_2)e_0R}$ 에 의하여 R이 작아지면 작아질수록 Bonding이 더 세짐.
• e.g. 반지름 : Na-F < Na-Cl (F가 Cl보다 작으므로)
• Melting point : NaF > NaCl

이온결합의 생성 과정

격자화 (Lattice)

• 1D crystal에서

  

• k : Madelung’s constant, 배열에 의해 결정되는 상수값

Covalent bond (공유결합)

• 수소 2개에서 $1s^1 \text{ 보다 } 1s^2$ 가 더 안정함.
• 각 오비탈에 전자를 하나씩 공유하면서 더 안정해짐.
• 이온결합: Attraction, Repulsion으로 클래시컬하게 설명가능, Covalent bond는 양자역학적으로 설명가능
• 공유결합에서의 Octet rule, (2, 8, 8, 8, 8 or 18) : 각각의 orbital에 전자를 공유하고 이 때 슈뢰딩거 방정식 계산했을 때 안정해짐.

공유결합에서의 Lewis structure and octet rules

• Lone pair : 결합에 참여하지 않은 최외각 전자쌍
• 각각의 원자가 옥텟룰을 만족하기 위한 전자의 수 계산, 현재 갖고 있는 전자의 합 계산, 그 둘의 차이를 뺀다음 /2를 하여 결합의 갯수를 계산.
• ex) $CO_2$ 의 경우 C, O 모두 옥텟 만족하기 위해서 8개의 전자 필요, C는 4개, O는 6개 보유. 즉 8 × 3 = 24개 전자 필요,, 4+6+6=16 개 전자 가짐 24 − 16 = 8, 8/2 = 4 개의 결합이 필요. 즉 C-O간에 이중결합.

Formal Charnge (형식 전하)

• 조건
  1. 공유결합을 가정
  2. 각 element에 charge를 배정
• 계산 : 원래 갖고 있던 전자 수 - (결합의 수) - (2×Lone pair의 수)
• Lewis structure에서 타당성 결정 : 형식전하의 절댓값이 작은 쪽 (균등하게 전하가 배분된 쪽) 이 안정함.

Resonance Structure

• 2개 이상의 structure가 모두 가능한 경우 Resonance하게 됨. 슈뢰딩거로 계산해봐도 구조가 서로 바뀌며 공유하는 것이 더 안정
• 매우 빠르고 안정적으로 일어나기 때문에 Particle in a box에서 두 box가 합쳐진 것 과 같게 됨.
• delocalized : 비편재화된 전자 분포

Exceptions to the Octet rule

1. Odd- electron molecules : 홀전자 가지는 경우

2. Octet-deficient molecule : $ BF_3$ → 형식전하 계산시 4개의 bonding이 되어야 하나 F의 Formal charge가 +가 되는 것은 안정하지 않음. → 전기음성도가 높은 원자의 형식전하는 -인 편이 더 안정적임.

   Octet 규칙이 절대적인 것은 아님. 더 안정한 방향으로 가는 것

3. Heavier elements (d-electron atoms) → 굳이 8개 채우지 않고 더 채워도 됨.

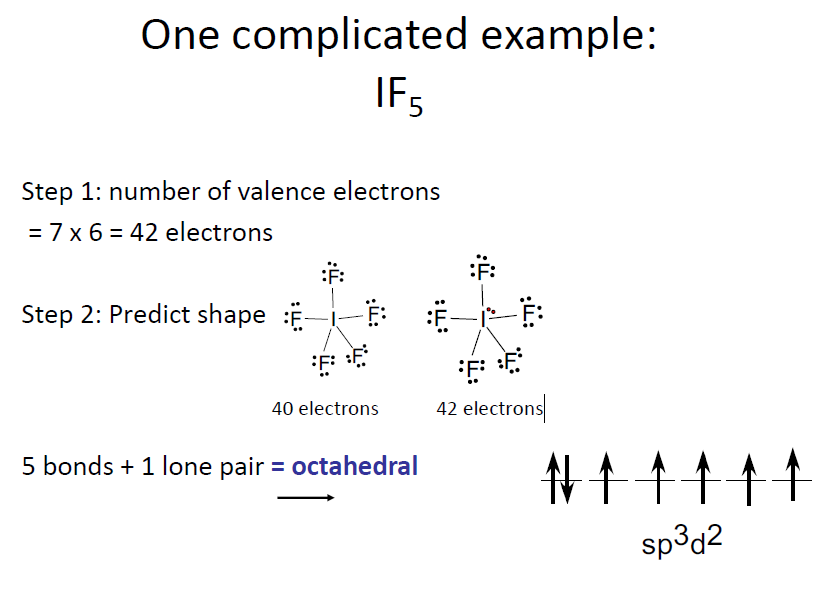
Valence shell expansion

• S : $1s^2 2s^2 2p^6 3s^2 3p^4$ : 이미 3s, 3p에 전자가 차있으므로 3d에 전자를 채우는 것이 큰 에너지적 손실이 아님.
• ex) $SF_6, PCl_5, ICl_4^-$

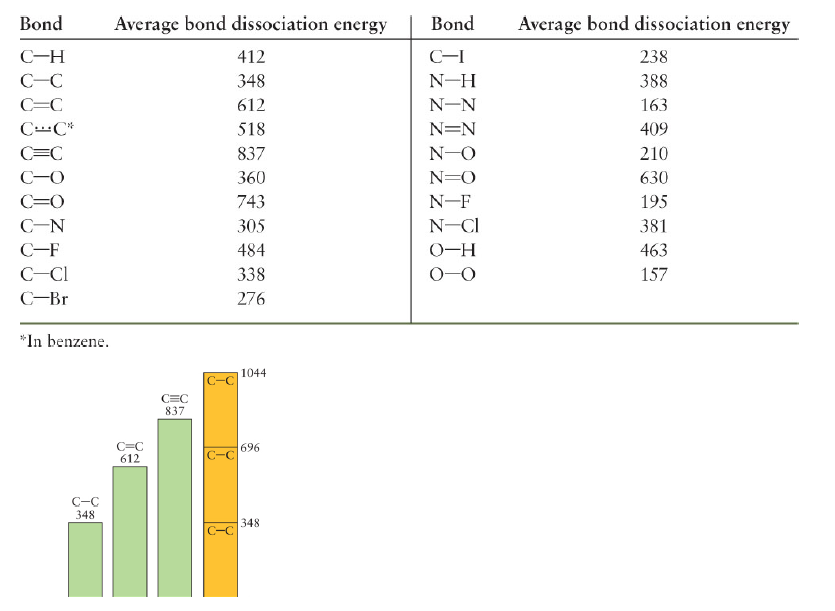
Covalent bond energy and length

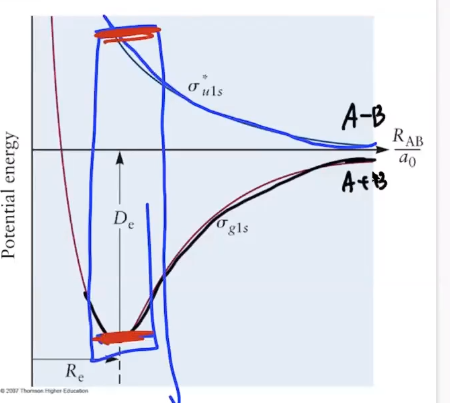
• D : AB를 A, B로 분리시키는데 필요한 에너지
• Bond length : 거리에 따른 퍼텐셜 그래프그렸을 때 최소인 지점
• 공유결합의 Bonding 에너지는 원자의 종류에 크게 의존하므로 종류에 따른 평균 에너지를 Table화 할 수 있음.

Polar covalent bonds (공유결합이지만 애매한 친구들)

• 완전히 전자를 가지고 갔다고 할수도 없고, 모두 공유한다고 할 수 도 없음.
• 두 원자가 각각 $δ^+, δ^-$, 즉 쌍극자 모멘트를 가지게 됨.
• 표시 : 두꺼운 화살표는 (-) 에서 (+) 방향, 얇은 화살표는 +에서 -
• Dipole moment $μ = δR$

VSEPR

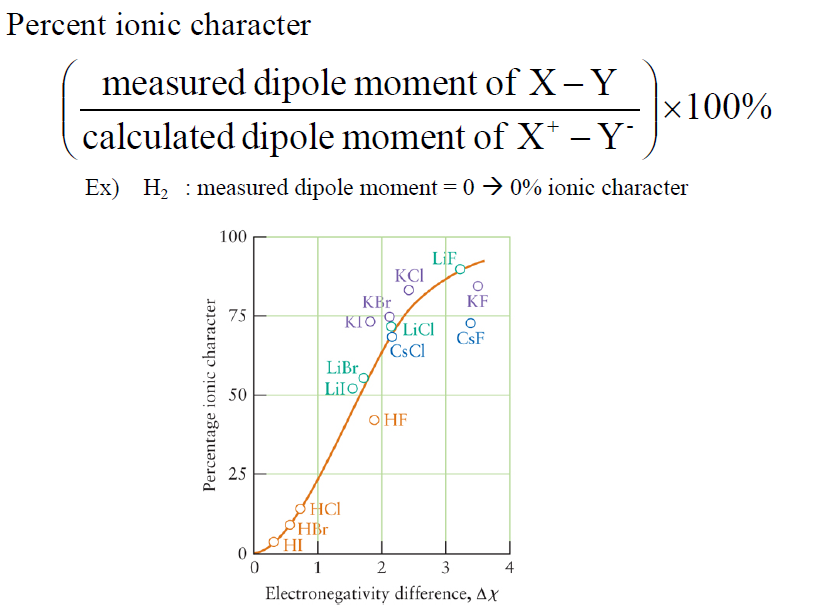
• Percentage of ioniccharacter

• 전기음성도의 차이가 클 수록 이온결합의 퍼센트가 높아지는 모습

Pauling’s Definition

• 전기음성도의 차이가 클 수록 ionic 할 것이다.]
• 실험적으로 ionic 결합이 covalent bonding보다 bond energy가 큰 것을 발견함.
• Pure covalent bonding이라고 가정을 하였을 때 실제 에너지가 이론적 에너지보다 크게 측정 → ionic한 경향 존재
• Expected (Pure covalent bond라고 가정하였을 때)의 bonding energy :

\[A-A \text{ bonding energy } + B-B \text{ bonding energy } \over 2\]

• 실제 Bonding 에너지에서 expected energy의 차가 전기음성도 차의 제곱과 같다.

Mulliken’s definition

• 특정 원소가 electronegative 하다 : Ionization energy가 큼 (전자를 많이 갖고 싶어 함으로 뺏기기 싫어함) + electron affinity가 큼 (전자를 추가로 더 갖고 싶어함)
• $\chi_A = {1\over2}(I.E+E.A)$

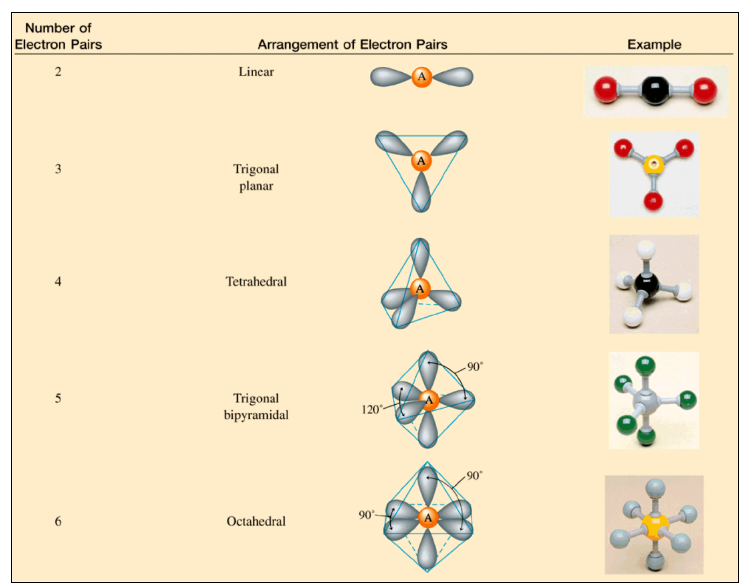
VSEPR Theory (Valence shell electron pair repulsion)

• 최외각 전자쌍들은 최대한 거리가 멀어지려고 함.

  

• 다른 것들은 다 대칭, But electron pairs가 5개인 Trigonal bipyramidal의 경우는 Equitorial, Axial로 서로 이루는 각이 다름.

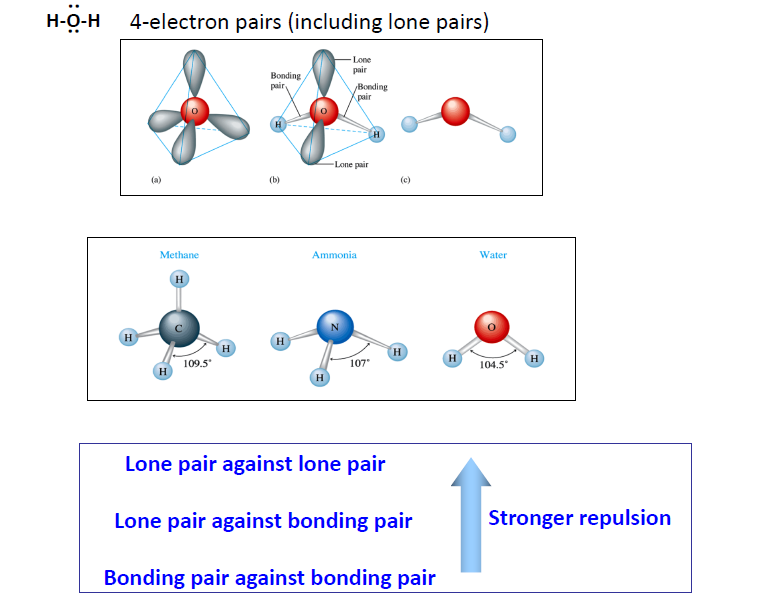
• Lone Pair의 반발력이 원자간의 반발력보다 조금 더 세기 때문에 Lone Pair의 갯수가 많아질 수록 각도 자체는 줄어듦.

  

• Bonding-Bonding < Bonding-Lone < Lone-Lone : 이로인해 $H_2O$의 H-O-H 각은 104.5도로 _CH_4의 109.5도, Ammonia의 107도보다 작음
• $XeF_4$ : 6 pairs : Octahedral → 비공유 전자쌍이 최대한 멀리 떨어지려면 서로 반대에 Lone pair 2쌍이 위치하는 것이 좋음 → 평면 구조
• $I_3−$ : 5 pairs : Trigonal bipyramid → Axial에 두 전자쌍이 위치하는 것이 좋음 → 직선형

• No-single central atom에 대한 예측 ex) $CH_3OH$

  

VBT (Valence band theory)

• 단일 결합과 이중, 삼중 결합은 왜 서로 에너지가 다른가. (정수배가 아닌가) → 단일결합에서의 결합과 추가적인 결합은 서로 차이가 존재.
• 이를 Orbital 간의 overlap으로 설명.
• H_2_S 에서 결합각이 VSEPR로는 완벽히 설명되지 않음. VB, 즉 오비탈간의 중첩을 이용하여 먼저 형상을 결정

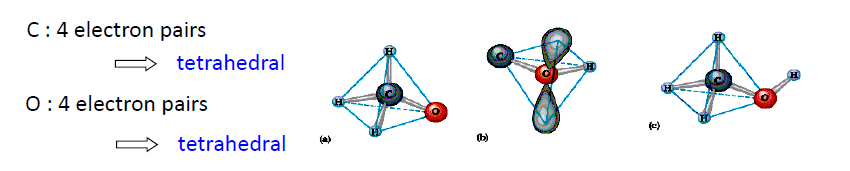
• CH 에서의 모순 : C의 Ground state : $\lbrack He\rbrack(2s)^2(2p_x)^1(2p_y)^1$ 이므로, H 2개가 각각 px 와 py 에 결합하여 결합각 90도 짜리 CH 를 이룰 것을 예상. BUT 실제로는 CH 는 불안정한 물질, Lewis 전자점식에 의한 CH 의 equivalent C-H Bond를 이야기할 수 없게 됨.

  

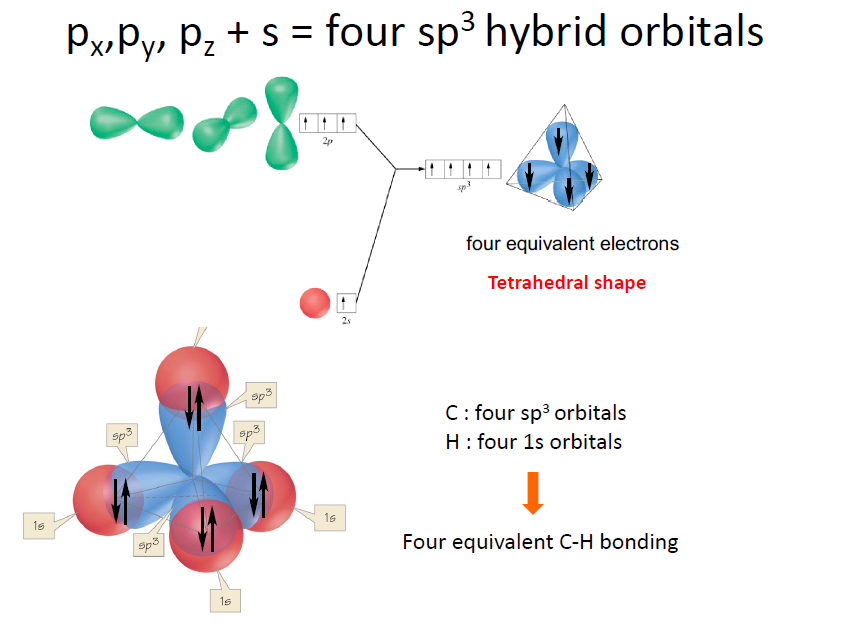
• s orbital 1개, p orbital 3개 (중심원자에서) 가 혼성화(hybridization) 되면서 4개의 동일한 _sp_3 orbital을 만들게 되고 각각에 수소 원자가 공유결합함.
• VBT의 규칙
  1. Number of hybrid orbitals = Number of atomic orbitals used.

  s 1개 + p 3개가 결합 → $sp^3$ 오비탈은 4개가 형성되어야 함

  1. Covalent bond 만들기 위해서는 atomic 혹은 hybrid orbital은 overlap을 만들어야 함.
  2. 분자의 모양은 Hybrid orbital의 배치에 의해 결정되며 이는 원래의 Atomic orbital 과는 달라야 함.
• 먼저 혼성화를 한다음 나중에 전자를 배치함.
• 슈뢰딩거 방정식을 풀어 만들어진 각각의 orbital 들은 각각 orthogonal함. 즉, 두 파동함수의 곱을 대수적으로 적분하였을 때의 값이 0이 나옴. 그렇기에 타당.
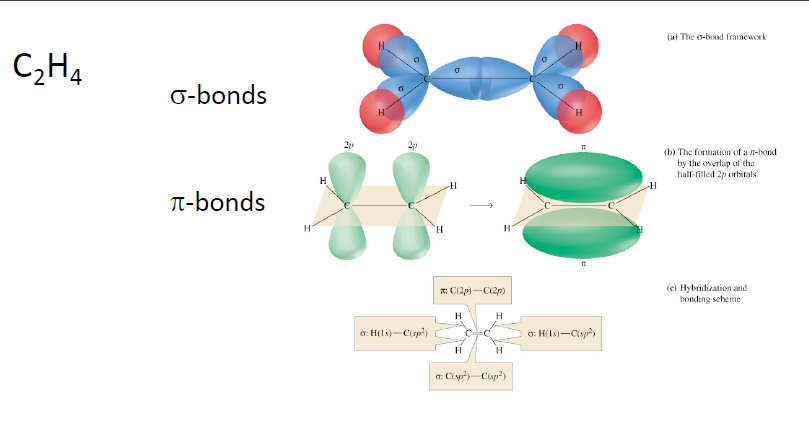
• $sp^2$ 간의 bonding: s, 3 * p 중 2개의 p가 $sp^2$ 결합에 참여, 남은 한개의 p는 수직하게 p와 p간의 결합을 형성 → $\pi$ bond라고 부르며, 일반적인 $\sigma$ bond 보다 조금 약함. 그 이유는 planar node를 형성하기 때문.

• Lewis structure : double bond는 identical single bond 2개로 설명, 부정확
• VBT : σ bonding 1개 + π bonding 1개로 설명.
• $dsp^3$ Hybridization : trigonal bypyramidal : one s + 3 p , one d
• $d^2sp^3$ Hybridization : octahedral : one s, 3 p, two d

• 예측하는 방법이 아닌, 이미 발견된 기하학적 구조를 설명하기 위한 이론.

  

MOT (Molecular Orbital Theory)

• LCAO (Linear Combination of atomic orbitals) : 분자의 파동함수는 각각을 구성하는 원자의 파동함수에 Coefficient를 곱하여 모두 더한 것과 같다.
• 분자의 파동함수 또한 존재확률 때문에 normalization 하면 1이 나와야 하므로 계수들의 제곱합은 1이어야함.
• Orthogonal해야 하므로 새로운 축을 만들었을 때도 크기가 1이 되게 만들어줘야 함.

Bonding MO, Anti-Bonding MO

• A-B molecule (1s, 1s의 결합)에서 2개의 solution이 존재: Bonding, Anti-bonding
• Bonding : $\Psi_1 = A(\phi_{1s, A}+\phi_{1s, B})$ - Constructive interference of two AOs
• Anti-Bonding : $\Psi_1 = A(\phi_{1s, A}-\phi_{1s, B})$ - Destructive interference of two AOs
• 파동함수끼리의 중첩에서 보강, 상쇄 간섭이 일어나며, 제곱합의 경우는 Anti-bonding인 경우에 node가 생기게 됨.
• node가 생김 : 에너지가 올라감. (결합이 약함.) / 두 원자 가운데 전자가 올 수가 없음.

• AO - MO 에서의 Diagram에서의 bonding, Anti-bonding의 에너지 준위.
• 즉 Bonding MO는 결합을 강하게, Anti-bonding MO는 결합을 약하게 만듬.
• Bond order = ${(\text{Bonding})-(\text{Antibonding})\over 2}$

• Core electron이 Bonding에 영향을 미치지 않는 이유

  

  • 애초에 bonding과 anti bonding의 갯수가 같아서 bond order에 영향을 주지도 않음.
  • n수가 작아 전자가 위치하는 반경이 원자핵과 가까움. 즉 실제 결합은 바깥쪽에서 일어나기 때문에 크게 영향 미치지 X
• 전자들은 각 원자에 종속되어 있는 것이 아니라 가운데 비편재화 되어있음(delocalized)

P orbital간의 Bonding

• 결합 축을 주로 z축으로 설정함

• $2p_z − 2p_z$의 결합 : σ bonding,

  

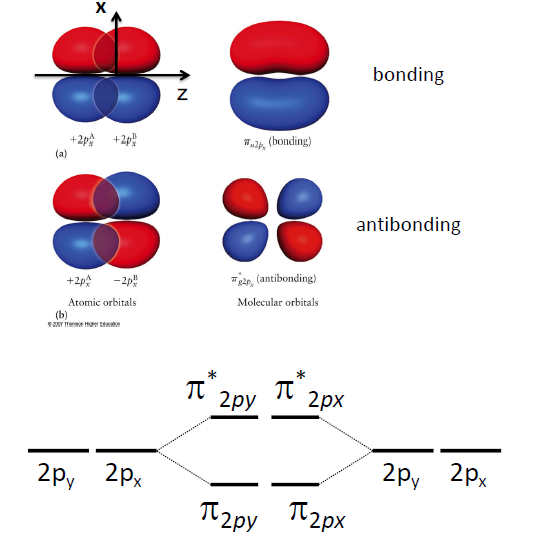
• $2p_x − 2p_x \text{ or } 2p_y − 2p_y$의 결합 : π bonding,

  

• px 와 py 는 degenerated (에너지 준위가 동일)
• 일반적으로는 σ 결합이 π 결합에 비해 안정함 ( π 결합은 node가 존재하므로)

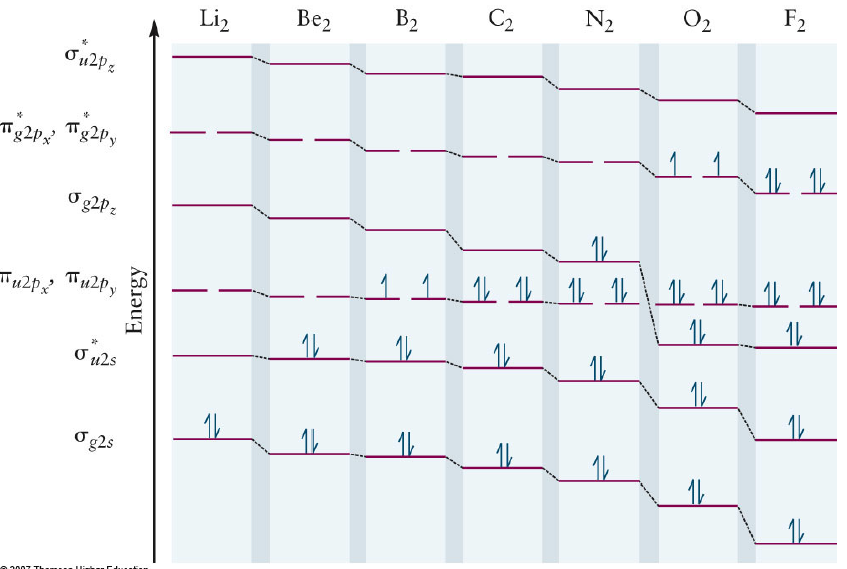
• 앞쪽이 이상한거, 뒤쪽이 정상적인 Order
• u, g 는 중심을 기준으로 점대칭성의 유무를 나타냄. π bond의 경우 Antibonding이 g, bonding이 u

예외사항 : bonding order가 반대가 됨. (B, C, N의 경우)

• B, C, N : 전자 자체가 많이 존재하지 않음
• 애초에 2s, 2p의 Energy level 차이를 증가시키는 요인은 shielding effect였으므로, B, C, N은 그 effect가 작아서 차이가 적음.
• 거리가 가깝기 대문에 2s, 2p orbital 간에 interaction 일어남

Bond order, length, energy의 관계

• Bond order가 높아짐 → 당연히 길이는 짧아지고 에너지는 높아짐.
• F constant : 용수철 상수 또한 bond order와 비례.

자성의 결정 (상자성, 반자성)

• M.O를 그렸을 때 Unpaired electron 존재하면 상자성(Paramagnetism)
• 그렇지 않으면 반자성(Diamagnetism) → 일반적인 물질은 약간의 반자성을 가지고 있음.
• Lewis 전자점식으로는 불가능, but M.O.에서는 증명가능.

Heteronuclear (different) diatomic molecules의 MO로의 설명

• 전기음성도 차이가 거의 없을 경우 homonuclear에서의 방법과 거의 유사하게 사용해도 됨.
• 전기음성도의 차이가 클 경우 그대로 적용하기 어려워짐

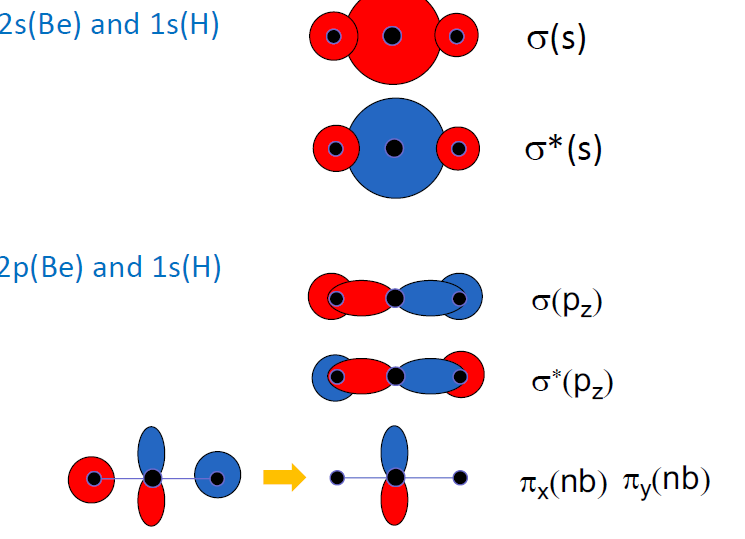
AO로부터 MO를 만들 때 적용되는 중요한 규칙들

1. 거의 비슷한 에너지 레벨의 오비탈끼리만 혼성이 가능.
2. 공간적으로 오버랩이 존재해야함. (e.g. core electron 같이 1s-1s의 중첩은 일어나지 않음)
3. correct symmetry (대칭성)
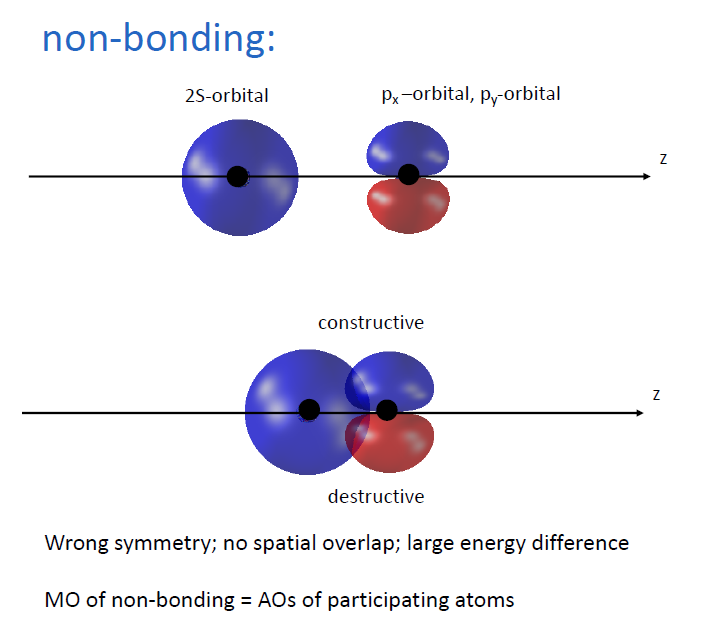
   • non-bonding의 예시 : 앞서 말한 규칙을 지키지 않은 경우

서로다른 원자간의 MO, (전기음성도 차이가 클 경우)

• 에너지 Diagram에서 아래쪽에 위치 : Vaccum level과의 차이가 큼 → IE가 큼, → EN이 큰 원소를 의미
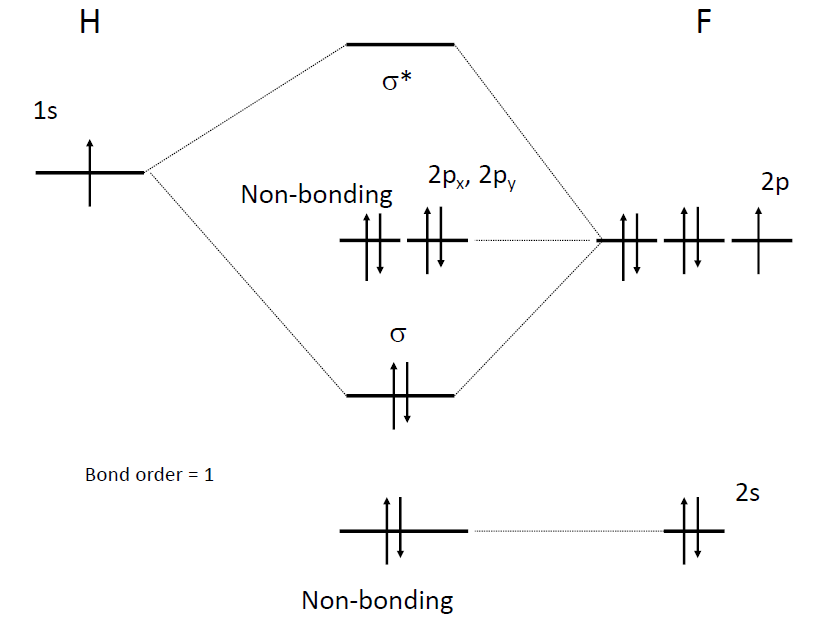
• HF의 Molecular orbital 예시

• H의 1s와 F의 2p가 에너지 준위가 비슷하므로 결합을 형성, 그 중에서 pz 만이 symmetry에 의해서 σ 와 σ_의 결합을 형성하며, 나머지 _px , py 는 non-bonding. F의 1s 또한 너무 에너지 준위 차이가 크므로 non-bonding

Relative energy of AO, and the resulting of MO

• 두 혼성하려는 오비탈의 에너지가 같은 경우 MO는 단순히 bonding은 더한다음 normalization, anti-bonding은 뺀 다음에 normalization 하면 됨. 즉 MO에 대해 AO의 기여도가 다 동일
• 에너지가 다른 경우 에너지가 더 높은 쪽 (vaccum쪽에 가까운 애)이 EN이 낮음 →anti-bonding과 에너지 준위가 가까움. 에너지 낮은 쪽이 EN이 높음, bonding과 가까움. 즉 가까운 쪽에 더 많이 기여하게 됨. 파동함수의 LCAO로 보았을 때 Coefficient가 큼
• Bonding orbital은 Electro negative한 쪽을 닮는다.
• 아예 차이가 클 경우 → non-bonding

MO of Polyatomic Molecule

• 동일한 규칙에 따라. (비슷한 에너지 준위, 물리적 겹칩, 대칭성)

• ex) $BeH_2$

  

• 위 그림처럼 됨, AO 쓴 갯수만큼 MO의 갯수가 생겨야 함.

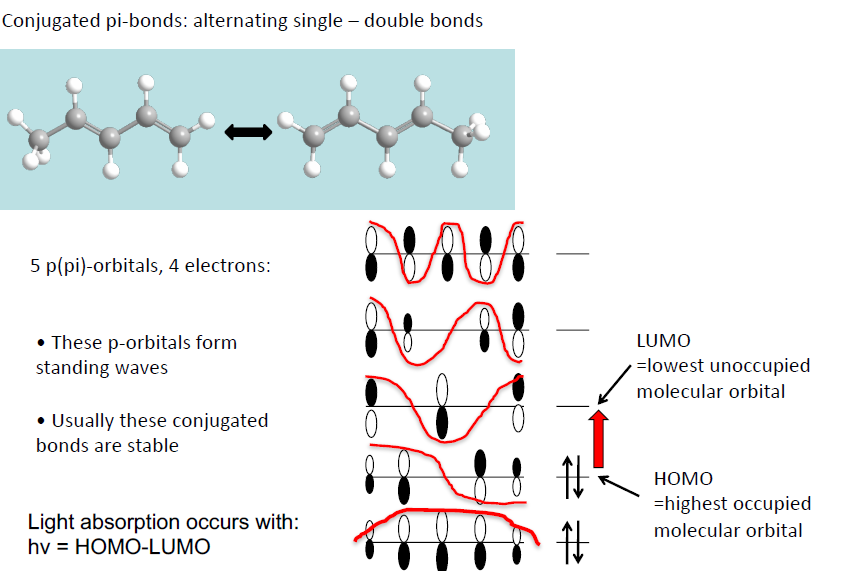
Conjugated Polyenes (탄소 사슬로 여러개 연결된 경우)

• s orbital끼리는 혼성이 안되나, px, py 끼리는 연결이 됨
• e.g. 5개의 C 고리로 이루어진 물질.

• 가능한 혼성의 조합에 대하여 나열할 수 있음, 안정한 순서는 node의 갯수가 적은 순서이며 particle in a box로 볼 수 있음

  

• Conjugated 물질에 대하여 HOMO, LUMO를 결정할 수 있으며, 이를 통해서 물질의 형광을 설명할 수 있음.