Post

[일반화학] Lec 02 - Atoms

Posted
Preview Image
By celenort
views 25 min read
[일반화학] Lec 02 - Atoms

전자기학

전자기파

  • 빛은 전기장과 자기장의 진동.
  • 라디오파, Microwave, 적외선, 가시광선, 자외선, X선, 감마선, 우주선 모두 전자기파이며 빛임.
  • 빛의 속도는 파장과 주파수의 곱이며 이는 일정. (광속불변의 원리)

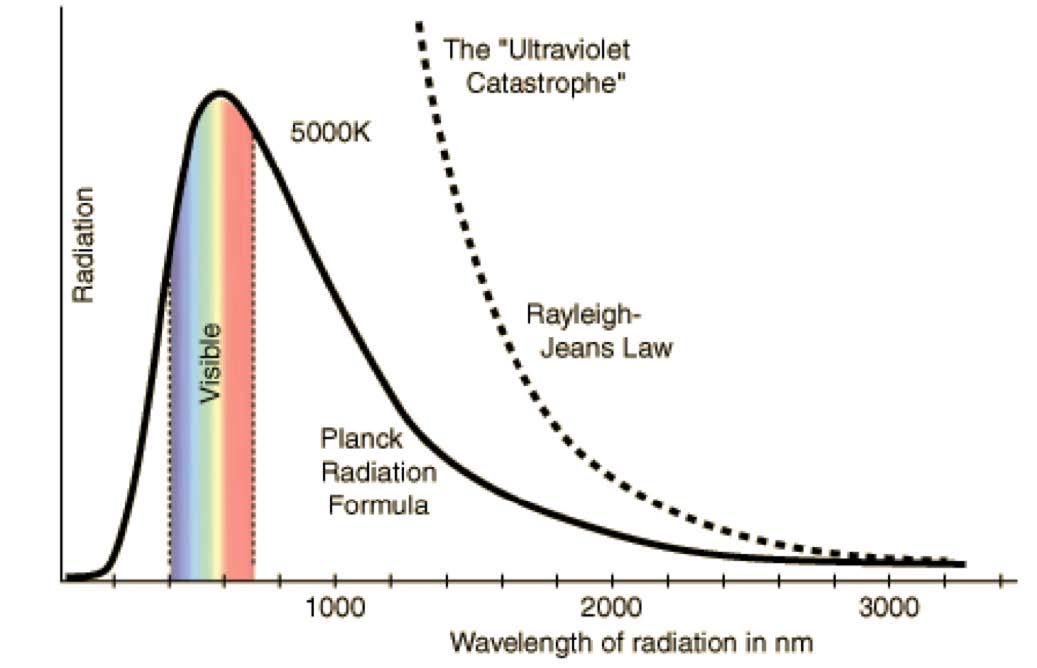
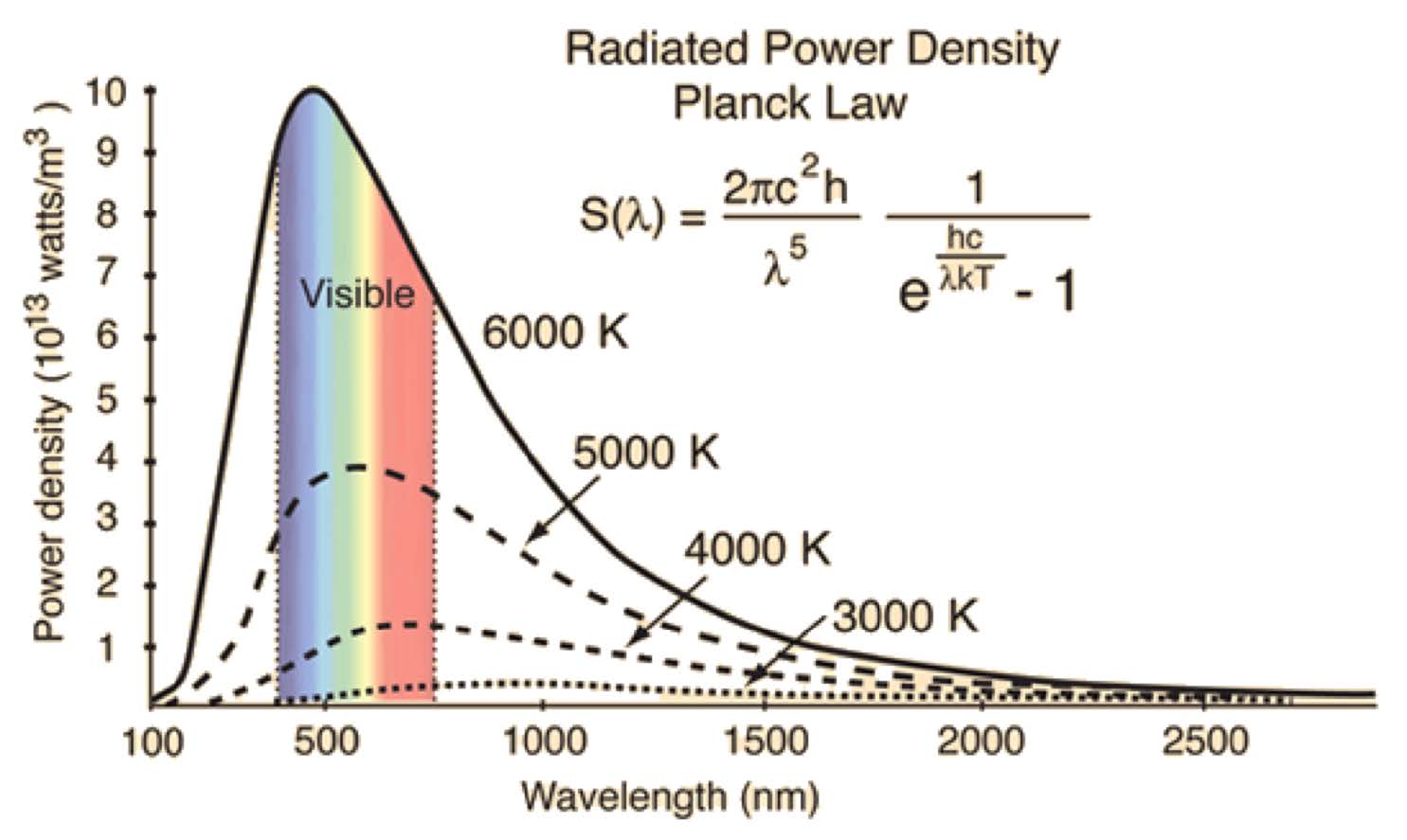
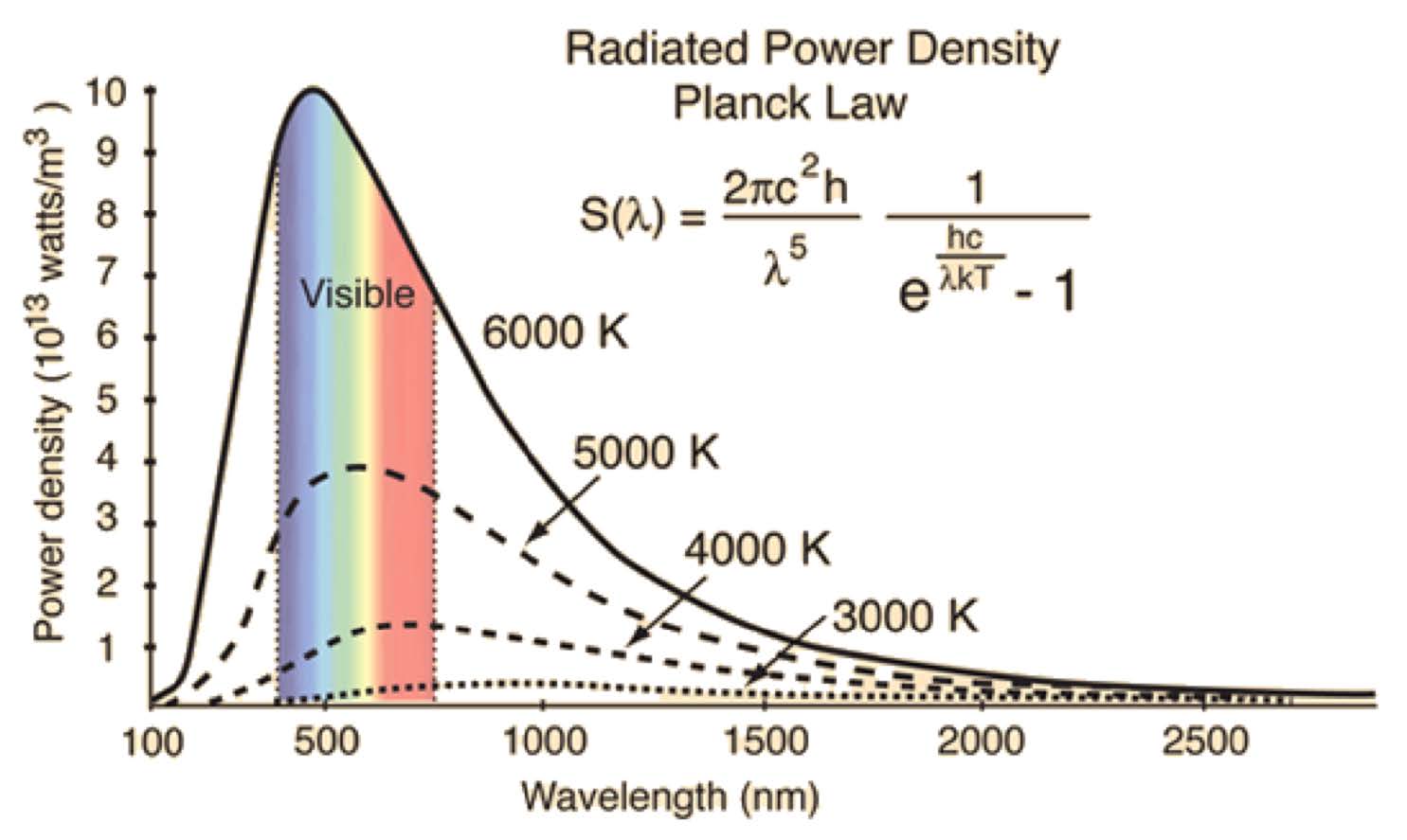
1. Black body Radiation (Max Planck)

  • 빛이 물체에 입사하면 빛은 투과하거나 흡수, 반사함.
  • ex) 물 : 외부 빛이 투과됨. / 색 : 빛이 흡수, 반사됨. (선택적 흡수와 반사에 따라 색 결정)
  • $E=hv$ 공식에 의해 빛에 의한 에너지가 온도를 올리는데 사용.
  • 흑체 : 들어오는 빛을 모두 흡수하도록 만들어둔 장치
  • 흑체 복사 : 모든 물체는 온도에 따라 각기 다른 파장으로 빛을 방출.

0

  • 온도가 내려갈 수록 Peak의 높이가 내려감. 흑체 복사하는 빛의 양 자체가 줄게 됨.
  • 육안으로 보이는 색 - 가시광선 영역에서의 Peak에 해당하는 wavelength의 빛. 즉 온도가 높을 수록 붉은 색 계열에서 푸른 색 계열의 빛으로 바뀌는 이유 설명가능

자외선 파국 (Ultraviolet Catastrophe)

1

  • 자외선 영역에서의 분포가 고전역학에서의 추론과 맞지 않은 부분 → 새로운 가설을 이용하여 설명하려 함
  • 파장이 작은 부분에서의 intensity가 무한대가 아닌 것을 설명하기 위해서 E=hv라는 빛의 입자성에 관련된 식을 도입해야만 함.

흑체 복사의 적용

  • 흑체는 들어오는 모든 빛을 흡수해야하나 현실적으로 검은색도 모든 가시광선 영역의 빛만 흡수하지 자외선, 적외선 영역을 흡수하지는 않음.
  • 태양을 비롯한 별의 경우 흑체라고 간주할 수 있음.

2

  • 태양은 지구에서 측정하면 빨간색으로 보임. → 대기 등에 의해 원래는 노란색인 것이 붉게 측정됨.

플랑크 상수

  • 자외선 파국을 해결하기 위해 실제 실험적 분포를 위한 가설을 세웠고, 이 가설을 만족시키기 위해서는 $E=hv$라는 공식을 무조건 만족해야함.

3

  • E=hv : 광자 하나에 대한 에너지, 빛이 진행할 때 광자가 따로따로 진행함

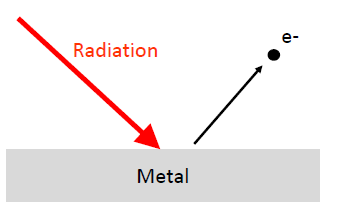
광전효과 (Photoelectric effect)

  • 금속에 전자를 조사하였을 때 빛의 세기를 늘려서는 전자가 튕겨나오지 않음. but 빛의 진동수를 높이면 전자가 금속 표면에서 튀어나옴.

4

  • 광전효과는 빛의 입자성(E=hv)를 증명하는데 중요한 근거가 됨. (광자가 가지고 있는 에너지는 frequency에 의해 결정)

5

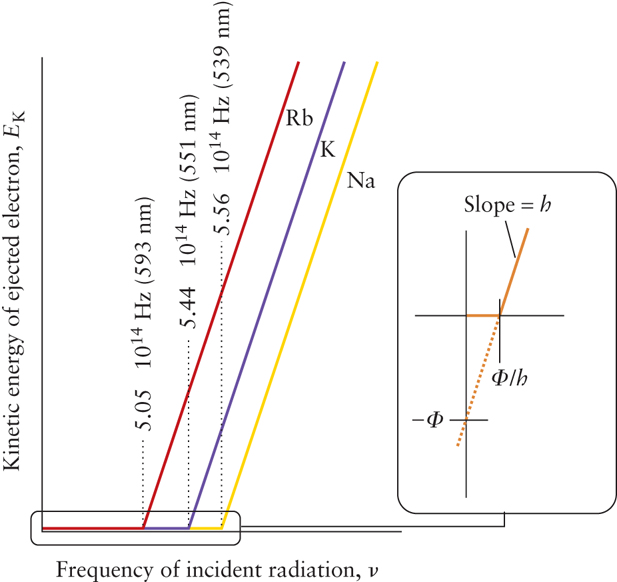
  • Work Function 이전의 에너지에 해당하는 freq의 빛을 조사하였을 때는 광전자가 튀어나오지 않다가, 금속 고유의 Work Function 이상의 hv에 해당하는 빛을 조사하면 광전자가 튀어나옴. 추가로 에너지를 더 주면 비례하게 전자의 운동에너지 증가.
  • Work Function은 금속마다 다르며, 튀어나가기 시작하는 지점 (onset) 이후에는 linear하게 운동에너지도 증가하게 됨. (그 기울기는 h임)
  • 광전효과로부터 얻을 수 있는 결론
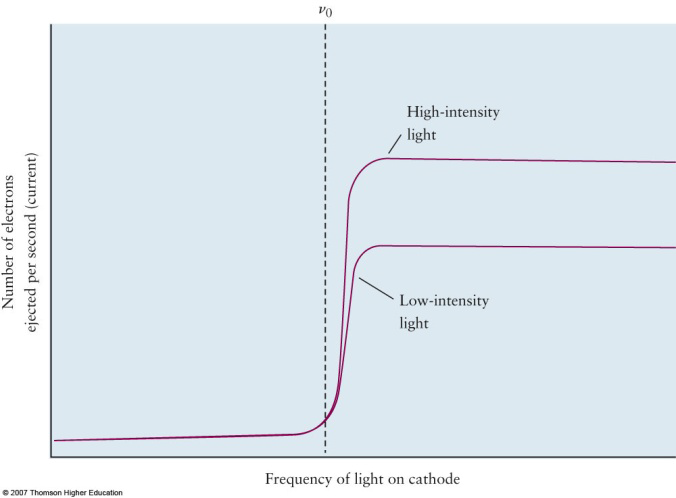
    • 전자의 Kinetic energy는 빛의 freq에 의존함.
    • 전자의 Kinetic energy는 빛의 세기에는 무관함.

    6

  • 동일한 금속(같은 일함수를 가지는)에 다른 세기의 빛 쬐여주면 광자를 방출하기 시작하는 frequency는 동일, intensity가 셀 수록 더 많은 양의 광전자가 빠져나옴.
  • 즉 빛의 입자성이 흑체복사와 광전효과라는 핵심적인 근거를 갖게 됨.

빛의 입자성과 파동성 (이중성)

  • 선 스펙트럼 (분광기) - 분광기를 통해 특정 원소를 방전관에 넣었을 때 발생하는 빛의 선 스펙트럼을 알 수 있음.

보어의 원자 모형

  • 원자에서 전자의 움직임을 설명하기 위한 두 가지 방법
    • 전자는 입자성을 띔 → 고전물리학적 법칙을 이용하여 설명 가능.
    • 전자는 파동성을 띔 → 전자가 빛은 아니지만 전자의 파동성도 광자와 같은 이유로 가능.

7

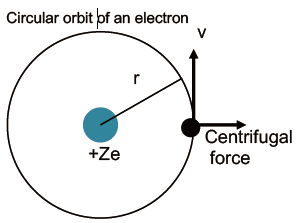
  • 중심에 (+) 전하, (-) 전하를 띈 공이 중심을 주위로 공전하고 있는 상황. 서로 충돌하거나 멀어지는 것이 아니라 같은 궤도로 계속 회전
  • Colombic Potential Energy(전위) :
\[V={ (+Ke)(e)\over4\pi \epsilon_0 r }\]
  • Total Energy : K.E + P.E
\[E_{Total}={1\over2}mv^2-{ Ke^2\over 4\pi \epsilon_0 r }\]
  • Total Energy=0 : Orbit할 필요 없음. - onset
  • Total Energy<0 : 구속되어있는 상태 - freq 낮음
  • Total Energy>0 : 원자 밖에 있는 상태 - freq 높음
  • 힘의 평형 : Centrifugal Force = Coulombic force
\[{m_e v^2\over r}={Ze^2\over 4 \pi \epsilon_0 r^2}\]
  • 각운동량은 양자화 되어 있음.
\[L = mvr = {nh\over 2 \pi}\]
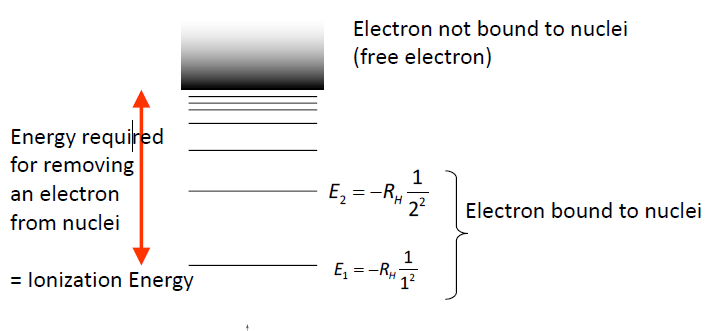
  • 보어의 가설 (각운동량이 양자화됨.) / 특정 $r$값만이 허용됨
  • r, E의 표현식

$r$을 $n, z$로 표현 :

\[r={\epsilon_0h^2\over Ze^2m\pi}n^2={a_0\over Z}n^2\]

$E$를 $n, r$로 표현, $n,z$로 표현

\[E = -{Ze^2\over 8\pi \epsilon_0 r} = {Z^2e^4m\over 8\epsilon_0^2h^2n^2}= -R_H {Z^2\over n^2}\]

$r$은 $n$의 제곱에 비례, $Z$에 반비례. $E$는 $n$이 커지면 증가 (0에 수렴, )

  • 원자에서 전자 방출 : 특정 파장의 빛을 주어야만 방출됨.

8

  • 수소 기체에서 이온화 에너지 : $n=1$에서의 전자의 에너지

De broglie’s explanation.

  • 물질파 : 빛도 파동이지만 입자성을 가짐. 물질도 파동성을 가질 수 있지 않을까?
\[\lambda = {h\over p}={h\over mv}\] \[\lambda = {2\pi r\over n}\]
  • 드브로이 + 보어의 (각운동량) 가설
  • 원주 / n = 파장.
  • 정상파 (circular standing wave)

9

  • 원의 원주를 n등분한 정상파로 나타내짐.

하이젠베르크의 불확정성 원리

\[\Delta p \times \Delta x \geq {h\over 4\pi}\]
  • 파동의 모양은 관측되지 않음. 그러나 파동함수의 제곱인 확률분포는 관측됨 (끝점과 가운데서 존재할 확률이 0)

슈뢰딩거 방정식 (시간에 무관한)

\[-{\hbar^2\over 2m}{d^2\over dx^2}\Psi(x)+V(x)\Psi(x)=E\Psi(x)\]
  • 전자, 파동 모두에 적용가능 (질량만 바뀌면 됨)
  • 위치함수, $x$에 관계있는
  • $V(x)$ : $x$의 위치에 따른 퍼텐셜, 각각 상태에 맞게 대입하면 됨.
  • $x$에 대해 2번 편미분한 것이 원래의 함수 → 삼각함수이어야만 함
\[\Psi(x) = Asin({2\pi\over \lambda}x)\]
  • $-{\hbar^2 \over 2m} $ 이 오퍼레이터(파동함수에 곱하여 에너지의 term으로 바꾸어주는 것) 인 이유
  • Ψ(x)를 미분하면 A, 진폭항에 $({2})^2 $
  • $= {hmv} , E_k={p^2\over 2m}$ 를 적용하면 맞음.
  • 슈뢰딩거 방정식의 앞부분 : 고전역학의 Kinetic Energy 에다가 파동함수를 곱한것과 동일.
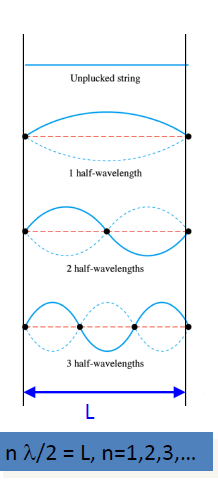
  • 슈뢰딩거 에너지에서 가장 낮은 에너지 준위 : 무한 퍼텐셜 벽에 파동이 걸치면 에너지가 높아지므로 양쪽 끝이 마디가 되게 해야 함. 즉 $\lambda = 2L, \lambda = L, …, \lambda= {2L\over n}$
  • 파동 자체를 추론할 수 있어도 측정은 불가, 그러나 측정할 수 있는 것은 파동함수의 제곱(확률분포) 이므로, 퍼텐셜 우물 전체에서 확률밀도함수의 적분값이 1이어야 함.(by definition)
  • $\therefore A =\sqrt{2 \over L}$

슈뢰딩거 방정식에서의 에너지

\[E_k = {1\over2}mv^2 = {p^2\over2m}={n^2h^2\over 4L^2}{1\over 2m} = {n^2h^2 \over 8mL^2}\]
  • Particle in a box에서 0~L의 범위에서 V(x) = 0이므로, $E_k = E$
  • 간격 : $E_{n+1}- E_n = (2n+1){h^2\over8mL^2}$
  • 거시세계 : 간격, 즉 계층화가 아주 작아 관측되지 않음. 질량이 작아야 계층화가 측정가능해짐.

슈뢰딩거 방정식의 분자에서의 적용

  • 분자의 길이가 긴 경우 vs 짧은 경우 :
    • 긴 경우 : Particle in a box에서 L이 큼, E자체는 작고, 간격 또한 좁음, 파장은 짧고 진동수는 큼
    • 짧은 경우 : Particle in a box에서 L이 작음, E 가 크고 간격 또한 큼. 파장은 길고 진동수는 짧음.
  • $E=hv$ 생각하면 됨
  • 분자의 길이가 짧으면 자외선 쪽, Blue 계열, 길면, 적외선 쪽, Red 계열의 빛

Hydrogen Atom에서의 파동함수(Orbital)

  • Particle in a box는 1차원에서의 파동함수, But 실제 원자에서는 r과 theta를 이용한 spherical coordinate를 사용하는것이 편리.
  • 변수분리 : $Ψ(x, y, z) = Ψ(x)Ψ(y)Ψ(z)$ 와 같은 꼴로 표현가능하면 이를 변수분리라고 함. 즉 구면좌표계에서는 R, Y, 즉 반지름에 관한 항과 각도에 관한 항의 곱으로 파동함수 표현 가능. 이 때 n, l, _m_을 이용하여 파동함수를 표현할 수 있음.

Quantum numbers

  1. $n$ (주양자수) = principal quantum number
    • Radius of orbit, n이 커질 수록 r이 커짐
    • 반지름, 에너지를 결정하는 양자수
  2. $l$ (각운동량 양자수) = Orbital angular momentum quantum number
    • 고전역학 : 모든 각운동량이 허용됨
    • 양자역학 : $l$ (각운동량 양자수) 또한 양자화(discrete)됨.
    • 각운동량을 결정함.
    • 각운동량 : $ l(l + 1)(h/2\pi)^2$
    • 즉 $l$은 각운동량 벡터의 크기를 결정
  3. $m$ (자기양자수) = magnatic quantum number
    • $L_z = m_l \times (h/2π)$
    • $m_l$이 양수이면 각운동량 벡터의 방향이 위쪽, 0이면 좌우 방향, 음수이면 아래 방향을 가리킴
    • $m_l$은 각운동량 벡터의 방향을 결정하는 요인 : 전자의 방향 : 자기장의 방향을 결정, 그렇기에 자기양자수라고 불림.

슈뢰딩거 방정식 풀기

  • Particle in the box에서 한 것 처럼 $n, l, m_l$에 관한 모든 가능성을 찾아보았더니..
  • n은 1, 2, 3 …
  • l은 0~n-1까지 가능 l=0, 1, 2 …에 각각 s, p ,d, f, g .. 오비탈의 이름을 붙임
  • ml은 -l ~ l까지 가능.
  • $Φ_{n,l,m_l}(r, θ, ϕ) = R_{n,l}(r)Y_{l,m_l}(θ, ϕ)$ 를 계산, 파동함수가 음양에 따라 (+) (-) 차이.

Orbital들의 에너지 준위

  • Particle in a box 의 에너지 준위와는 다르게 점점 폭이 커지지는 않음. 그러나 n=1, 2, 점점 증가함에 따라 계층화 되어있으며, 점점 0에 가까워지는 방향으로.

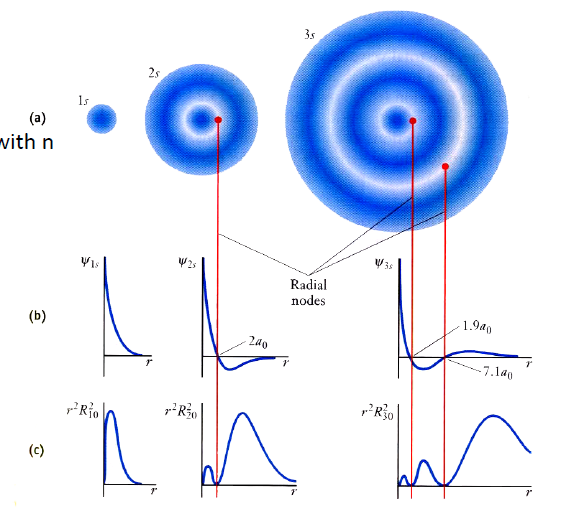
전자의 r에 대한 분포

  • x축이 r이 아닌 $4πr^2r$이어야 함.
  • node : 파동함수의 부호가 바뀌는 지점. (Particle in a box에서는 0에 닿는 부분. )
  • node가 많아진다 : 에너지가 높아진다. → 주어진 거리에서 파장이 짧아지므로 에너지가 높아진다.

10

  • n이 커질 수록 r이 커진다고 하는 이유 : 거리에 따른 전자의 분포, 즉 확률밀도 함수를 그렸을 때 n이 커짐에 따라 전자가 가장 많이 분포한 곳의 r 값이 커짐.

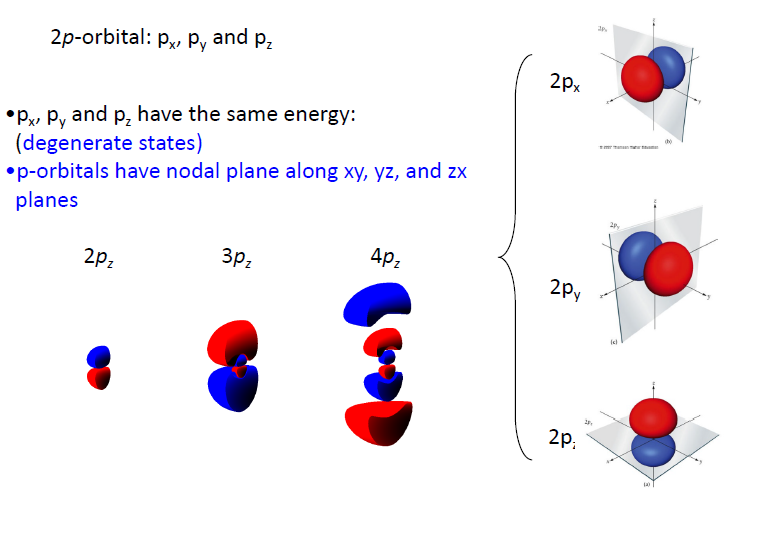
p orbital

  • $p_x, p_y, p_z$ have the same energy (only in H-atom)

  • 2p, 3p, 4p 가면서 node가 생기고 +와 -의 부호가 바뀌는 부분이 생김

    11

  • 또한 에너지적 측면에서 2p < 3p < 4p
  • P.I.B 관점에서 생각해 봤을 때 n이 커진다 → L이 길어진다. 에너지가 낮아진다 생각할 수 있지만, n이 커짐에 따라 node가 많아짐, 파장은 짧아지므로 전체적으로 에너지는 커진다고 볼 수 있음.

d orbital

  • $ d_{xy}, d_{yz}, d_{zx}, d_{x2}, d_{z^2} $의 5개가 존재하며, m = ±2, ±1, 0 이므로.
  • $xy, yz, zx$의 경우는 해당 plane 위에 orbital이 놓인 모양
  • $x^2 − y^2$는 x축, y축에서 보았을 때 각각 같은 부호의 orbital
  • $z^2$의 경우는 z축에서 보았을 때 같은 부호의 orbital이므로 이렇게 명명함.

전자가 어떻게 배치되는지?

  • 전자의 배치는 전자라는 입자의 성질 (fermion인지 boson인지에 따라 결정)
  • 전자는 fermion이기 때문에 스핀이 $\pm {1\over2}$ 을 가지기 떄문에, 서로 다른 스핀의 전자 2개만이 하나의 오비탈에 들어갈 수 있음.
  • 빛, 광자의 경우는 boson이기 때문에 spin이 0, 한 에너지 준위에 대해서 무한정으로 광자가 들어갈 수 있음.

  • 스핀의 발견

    12

  • 전체 파동함수의 앞에 상수로 ms 즉, 해당 전자가 +1/2 스핀인지 -1/2 스핀인지가 계수처럼 붙게 됨. Total Wave function of an electron of atom
  • $Φ_{n, l, ml, ms}(r, θ, ϕ) = F(ms)Ψ_{n, l, ml}(r, θ, ϕ)$
  • 전자 배치의 Rule : Pauli’s exclusion principle

한 Atom에서 $n, l, m_l, m_s$가 모두 같은 전자는 존재할 수 없다.

오비탈 간의 에너지 준위 비교

  • Hydrogenic Atom (전자가 한개만 존재할 때) : n, 주양자수의 크기에 따라서만 에너지 준위가 결정. 즉 2p, 2s간의 에너지 준위가 동일
  • Polyelectronic Atom (전자가 여러개 존재할 때) : 각각의 전자들간의 반발력으로 인해 에너지 준위가 달라짐. 이는 파동함수에서 R, Y가 단순히 n,l, l,ml에 독립적으로 연관되어있지 않아서 생김. 이는 전자 하나의 퍼텐셜 에너지 과정에서 그 정의가 달라지면서 생기고, $Z_eff$를 이용해서 보정.
  • $E_{ns} < E_{np} < E_{nd} < E_{nf}$
  • 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s …
  • Aufbau Principle : 가장 에너지 준위가 낮은 오비탈부터 전자가 채워지기 시작함
  • Hund’s Rule : Pairing 보다는 Unpair 되는 것이 선호된다.

유효핵전하의 계산

  • Hatree : Z 대신에 여러 전자가 들어갈 때는 $Z_{eff}$를 이용하자.
  • Shielding Effect : 가리움 효과.
  • Z → $Z_{eff}$ 로 바뀌었다 하더라도 에너지가 양자화 되어있다는 사실은 동일.
  • 다전자 원자에서 오비탈의 l값에 따라 에너지가 달라지는 이유 : $ E= -{Z^2\over n^2} R$ 로부터 에너지 자체의 식은 동일, 2p, 2s라고 생각해보면 n 값은 동일하나 Zeff 의 값이 달라지기 때문에 에너지 준위도 달라진다고 생각.

13

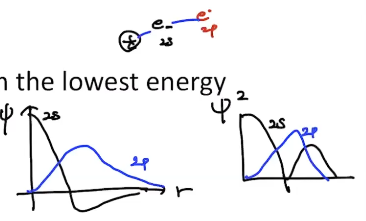
  • 2s, 2p에 의 확률밀도 함수에서 전자 밀도가 가장 높은곳이 2s오비탈이 2p오비탈보다 가까운 곳에 있기 때문에 2s가 2p를 밀어내게 됨 : 2s orbital의 penetration effect
  • 이러한 이유에서 s > p > d > f 순으로 에너지 준위가 올라감.

화학 반응

  • 최외각 전자(Valance Electron)만 반응에 참여, 내부 전자(Core electron)들은 반응에 참여하지 않음.
  • 3p를 모두 채운 이후에 (Ar 이후) 3d를 채우는 것이 아니라 4s를 먼저 채움.
  • 3d 오비탈의 경우 $4s^23d^4 \text{ or } 4s^23d^9$ 가 아닌 3d 오비탈을 먼저 채운 뒤에 s 채움 (비록 에너지 준위는 3d가 더 높지만)

이온들의 크기 비교

  • 양이온 : Cation, 음이온 : Anion 이라 부름

  • 같은 전자 배치 / +의 숫자가 커지면 커질 수록 이온의 반지름은 작아짐.

    $O^{2−} > F^− > Ne > Na^+ > Mg^{2+}$

  • 같은 (+)전하의 갯수 / 전자의 갯수가 커지면 그 다음 전자는 shielding effect에 의해 Zeff가 작아지고, 이로 인해 더 먼 궤도를 돌게 됨 : 전자의 갯수가 많아질 수록 이온의 반지름은 커짐

  • 원자의 크기 비교

    같은 주기에서 족이 커질 수록 반지름이 작아짐. (+)가 증가하는 것에 의해
    같은 족에서 주기가 커질수록 반지름이 커짐. 다음 오비탈을 채우기 때문에 반지름 커짐

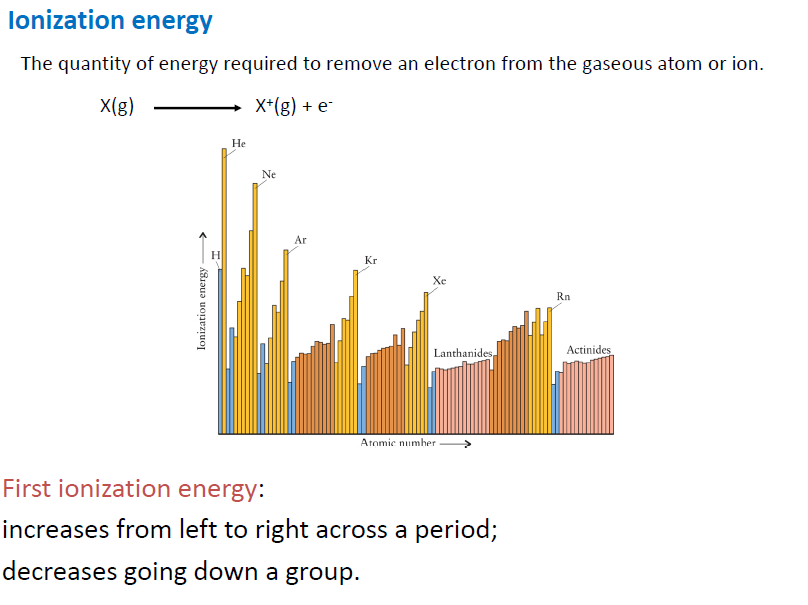
이온화 에너지 (I.E)

  • I.E, E.A 모두 gas 기준

14

  • 어느정도 원자 반지름과 관련성을 가지고 있음.
  • 더 큰 족으로 갈 수록 이온화 에너지 증가 (+)가 많아져 Zeff가 커지므로
  • 다음 주기로 갈 수록 이온화 에너지 감소. 다음 shell에 전자가 들어가므로 빼기 쉬움

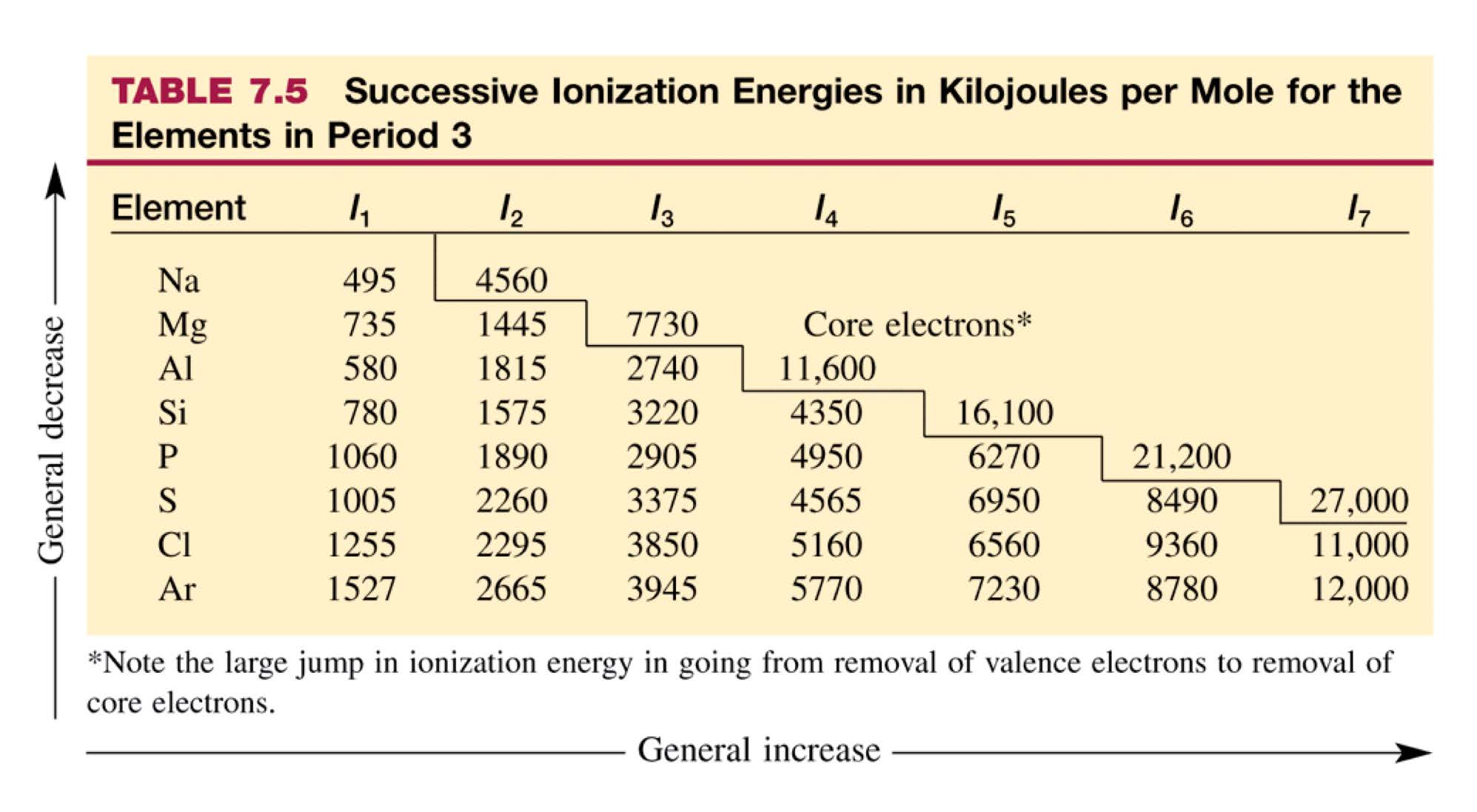
  • Multiple Ionization Energy : 큰 폭으로 이온화 에너지가 증가하는 것을 보고 전자의 오비탈이 달라졌구나 생각할 수 있음.

    15

  • 원자번호가 커질수록 더 커짐. (Na+보다 Mg2+가 더 작으므로)

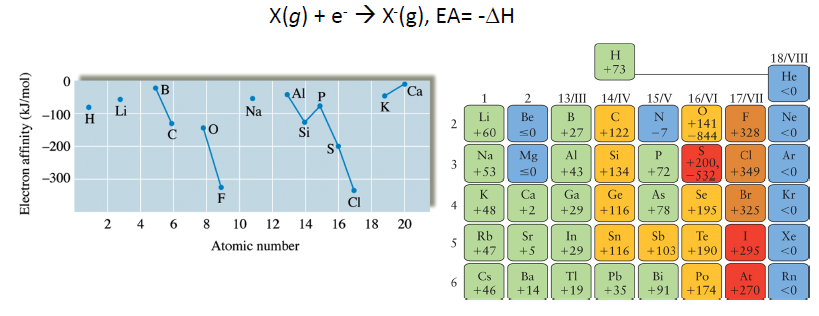
전자 친화도 (E.A)

  • 자발적 반응 : 에너지 방출되면서 안정해지는 것. / 비자발적 반응 : 에너지 흡수하면서 불안정해짐.
  • 전자 친화도 : 해당 원자가 전자를 하나 흡수하였을 때 안정해지는 정도 (에너지 관점에서)

16

  • 오른쪽 그림에서 + → 해당 값 만큼 안정해짐. - → 전자간의 반발력 때문에 =값이 나타나게 됨
  • 원자 반지름과도 연관. 원자 반지름이 작을 수록 전자 하나가 들어왔을 때 더 원자핵과 가까이 인접하여 안정해지므로 전자친화도 값이 큼. but 너무 작을 경우 전자간의 반발력 또한 커지므로 F< Cl임
  • EA가 +값이라고 할지라도 전자를 다른 원자로부터 가져와야 하는 것임.
  • 이온화 에너지, 전자친화도의 합을 구해서 에너지가 필요하다는 결론이 나와도 양이온과 음이온간의 인력 (격자에너지) 에 의해 안정해짐.
Lecture, 일반화학
화학 흑체 플랑크 불확정성 원리 오비탈
This post is licensed under CC BY 4.0 by the author.