[유체역학] Chap 3

Chapter 3.

유체 정역학 기본 방정식.

• dx, dy, dz의 미소 정육면체에 대한 미소체적 dV, 미소질량 dm
• $ dm = \rho dV $
• Body force :

\[d \vec{F}_B = \vec{g} dm = \vec{g} \rho dV = \rho \vec{g} dxdydz\]

• Surface force :

at $-yz $ plane

\[P = p_0 + {\partial p \over \partial y} (y_L-y) = p_0 + {\partial p \over \partial y} (-{dy \over 2})\]

• summing up all forces,

\[d\vec{F}_s = -({\partial p \over \partial x}\hat{i}+{\partial p \over \partial y}\hat{j}+{\partial p \over \partial z}\hat{k} )dxdydz = -\nabla P dxdydz\]

• combining with body force,

\[d\vec{F} = (-\nabla P + \rho \vec{g})dxdydz\]

• 깍두기는 힘의 평형 상태에 있으므로,

\[\nabla P = \rho \vec{g}\] \[{dP\over dz} = -\rho g= -\gamma\]

• Constraints
  1. 정지유체
  2. 유일한 체적력(Body force) : Gravity
  3. z축이 수직, 위방향.

Gauge pressure

\[P_{abs} = P_{gage} + p_0\]

Manometer

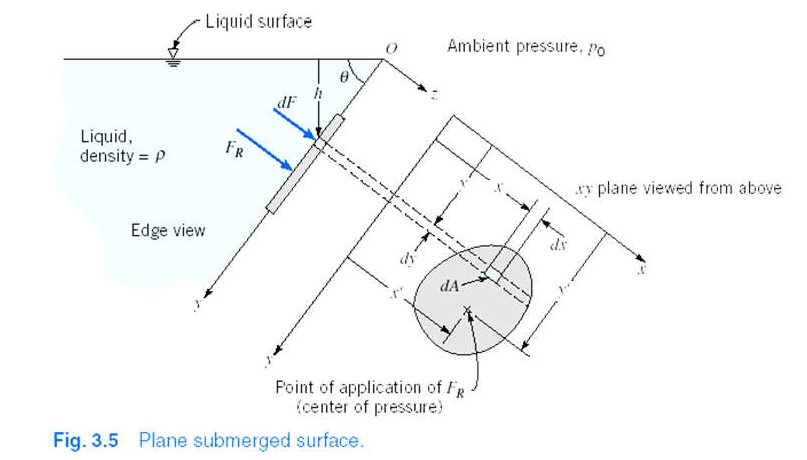
\[\Delta P = g \Sigma_i \rho_i h_i\]

Plane Submerged Surface

\[dF = pdA = (p_0 + \rho gh)dA = (p_0 + \rho gy \sin{\theta})dA\] \[F_R = \int_A \rho dA = \int_A p_0 dA + \int_A \rho gy \sin{\theta} dA\] \[= p_0 A + \rho g \sin{\theta} \int{ydA} = p_0 A + \rho g \sin{\theta} y_c A\] \[\therefore F_R = p_0 A + \rho g \sin{\theta} y_c A = (p_0 + \rho g h_c) A\] \[y' \cdot F_R = \int y dF = \int y PdA\] \[\int p_0 y dA + \int \rho g \sin{\theta} y^2 dA\] \[p_0 y_cA + \rho g\sin{\theta} I_{xx}\]

• 평행축 정리, $I_{xx} = I_{\hat{x}\hat{x} }+Ay_c^2$

\[y' \cdot A(p_0 + \rho g h_c) = p_0 Ay_c + \rho g \sin{\theta} I_{xx}+\rho g \sin{\theta} A y_c^2\] \[y' = y_c + {\rho g \sin{\theta}I_{\hat{x}\hat{x} } \over Ay_c (p_0+\rho g h_c)}\]

• 반대쪽에도 $ p_0$의 압력이 작용한다면?

\[y'=y_c + {I_{\hat{x}\hat{x} }\over Ay_c}\]

• Similarly $x$축 :

\[x' \cdot F_R = \int xdF = \int x(p_0+\rho g \sin{\theta}y)dA\] \[= p_0 \int xdA + \rho g \sin{\theta}\int xydA\] \[= x_c(p_0 + \rho g y_c\sin{\theta}) A + \rho g \sin{\theta}I{\hat{x}\hat{y} }\] \[\therefore x' = x_c + {\rho g \sin{\theta}I_{\hat{x}\hat{y} }\over F_R}\]

Hydrostatic force on a curved submerged surface

• Horizontal : $ F_H = p_c \cdot A $
• 정사영 했을 때의 centroid에서의 pressure, 전체 Area
• Vertical : $ F_V \rho g V $
• 해당 면 위의 $V$만큼의 중력을 받음.

부력과 안정성

\[F_z = \int dF_z = \int_{V} \rho g dV = \rho g V\]