[유체역학] Chap 1, 2

Chapter 1.

유체역학의 기본 지배방정식

1. Conversion of mass
2. Newton’s 2nd Law
3. Conversion of Angular Momentum
4. 1st law of Thermodynamics
5. 2nd law of Thermodynamics

Solid vs Fluid

• Solid : deform or bend -> elasticy
• Fluid : continuously deform -> viscosity

Methods of Analysis

System

• Closed System (system)
• Open System (Control Volume)

기술 방법

• Lagrangian approach : 입자의 궤적을 추적하는 기술법
• Eularian approach : Attention on properties of flow at a given point in space in function of time.

접근법(Approach)

• 미분접근법(differential) : 나무에 집중. ex) 날개 표면의 압력 분포
• 적분접근법(Integral) : 숲에 집중. ex)전체 양력

Chapter 2.

Fluid as continuum

• 미소 부피 $ \delta V $ , 미소 질량 $ \delta m $ 에 대해서
• 이 미소 체적에 대한 질량/부피, 즉 밀도가 일정해지는 최소체적 이상을 연속체로 간주.
• 일반적인 희박기체가 아닌 유체에 대해서는 연속체로 가정해도 무방.

Velocity Field

• $ \vec{V} = \vec{V}(x,y,z,t) $

Steady Flow

• $ { {\delta \eta}\over{\delta t} } = 0 , \eta $ : properties of fluid
• 일 때 정상 유동, Steady flow라고 명명.

One/Two/Three Dimension flow

• $u(r)$ : 1-D Flow
• $u(r,x)$ : 2-D Flow

Lines

Timelines (시간선)

• set of fluid particles that form a line at given instant.
• ex) 도로 위 차량들이 이루는 선.

Pathline (유적선)

• actual path travesed by a gives particle.
• $ {dx \over dt}\rparen _{particle} = u(x,y,t) $
• $ {dy \over dt}\rparen _{particle} = v(x,y,t) $

Streakline (유맥선)

• locus of particles that have earlier passed through a prescribed point
• 특정 점을 통과하는 입자에 표식을 남기고 표식이 남은 입자끼리 연결한 선.

Streamline (유선)

• a line everywhere tangent to the veolcity vector at a given instant
• 유선은 모든 속도 vector 접선이고, 유선을 가로지르는 유동은 일어나지 않음.

\[{dy \over dx}\rparen _{stream} = {v(x,y)\over u(x,y)}\]

at steady flow

• Timeline = Pathline = Streakline = Streamline

Stress field

• 표면력(Surface force) : Pressure, Friction
• 체적력(body force) : gravitational force, electromagnatic force
• Surface force -> Stress(응력)
• Normal / shear force : $ \tau_{xy} $
• x : plane on which stress acts / y : direction in which stress acts

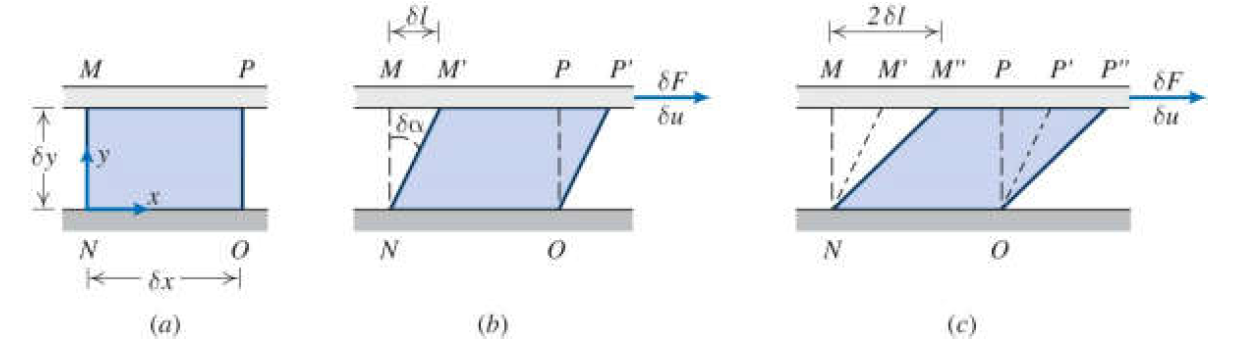
Defrormation

• 변형률 (deformation rate) :

\[\lim\limits_{\delta t \rightarrow 0 } {\delta \alpha \over \delta t} = {d \alpha \over dt}\]

• $ \delta l = \delta u \delta t = \delta y \delta \alpha $
• deformation rate = $ {du \over dy} $
• shear force $ \tau \propto {d \alpha \over dt} $ , 이러한 선형 관계를 만족시키는 유체를 Newtonian fluid라 함.
• 이 때의 계수 $ \mu $ : Dynamic, Absolute Viscosity.

\[\tau_{yx} = \mu {du \over dy}\]

Classification

• 연속체 Fluid dynamics
• 점성 / 비점성 ($ \mu =0,\neq 0 $)
• 비점성일 경우 층류(laminar) / 난류(turbulant)
• 압축성, 비압축성 유동(compressible, incompressible)
• 내부유동, 외부유동

Reynolds 수

\[Re = \rho {VL \over \mu}\]

• 특성 Veolcity, Length, density, viscosity를 대입.
• 클 경우 점성에 의한 영향을 무시 가능, 작을 경우 점성이 지배적임.

d’Alembert의 역설

• 점성이 없는 비점성(invicid) 유동의 역설로, 모든 물체에 항력이 존재할 수 없음.

Prandtl (d’Alembert’s Paradox 해결)

• viscous boundary layer를 전후로 Reynolds수가 충분히 큰 경우에도 경계에서는 점성이 지배적인 유동이 나타남.

Pressure drag

• 경계와의 마찰이 후류(wake)를 만들어 냄.
• 역압력, 지나갈 수록 입자의 속도는 줄어들고, 속도가 멈추는 시점에서 유선을 따라가지 않고 후류를 생성하게 됨. (박리점 이후)
• 이로 인한 항력을 압력, 형상 항력이라 부름. (Pressure drag, form drag)
• Streamlining - 유선 간격이 점진적으로 넓어지도록 함 -> form drag를 줄일 수 있음. (역압력 구배와 후류가 줄어들기 때문.)

Laminar, turbulant

• $ \vec{V} = u \hat{i} $ : laminar
• $ \vec{V} = (\overline{u}+u’) \hat{i} + \overline{v} \hat{j} + \overline{w} \hat{k} $ : turbulant : 무작위적 운동.

Internal, External flow

• Pipe 에서의 유동 : Internal flow. 검사체적이 닫혀있음. $ Re = \rho {\overline{v} D \over \mu} $
• 무한 유체 속에서의 운동 : External flow. $ Re_x = \rho {U_{\inf} x \over \mu} $

Compressible, incompressible 유동.

• Compressible -> Water Hammer (수격작용), Cavitation (공동현상) 등 일으킴.
• Mach number : $ M \equiv {V \over c} $ 공기의 경우 0.3을 기준으로 이보다 클 경우 압축성, 작을 경우 비압축성으로 취급.
• $c$ : 상대 음속