[동역학] Tangential, Normal components of moving particle

Tangential and normal components

\[\boldsymbol{v} = v \boldsymbol{e_t} \\ \boldsymbol {a} = {dv \over dt} \boldsymbol{e_t} + {v^2 \over \rho} \boldsymbol{e_n}\]

• 증명을 위해, $d\vec{e_t} / d\theta$ 를 구해보자.
• $\Delta \theta$ 동안 tangential 방향의 unit vector를 이용해 삼각형을 만들면, 두 벡터의 차가 $\Delta e_t$임.

\[\Delta e_t = 2\sin{\Delta \theta / 2}\] \[\lim\limits_{\Delta \theta \rightarrow 0} {\Delta \vec{e_t} \over \Delta \theta} = \lim\limits_{\Delta \theta \rightarrow 0} {\sin{\Delta \theta / 2} \over \Delta \theta / 2} \vec{e_n} = \vec{e_n}\] \[\vec {e_n} = {d\vec{e_t}\over d\theta}\]

Proof :

\[\vec a = {d\vec{v} \over dt} = {dv\over dt} \vec{e_t} + v {d\vec{e_t} \over dt}\] \[= {dv\over dt} \vec{e_t} + v {d\vec{e_t} \over d\theta} {d\theta \over ds} {ds \over dt}\]

by geometrical insight,

\[\rho d\theta = ds\] \[\vec{a}= {dv\over dt} \vec{e_t} + v \cdot {1\over \rho} \cdot v \cdot \vec{e_n}\] \[\therefore \vec{a} = {dv \over dt} \vec{e_t} + {v^2\over \rho} \vec{e_n}\]

Tangential and Normal compoenets in 3-dimension

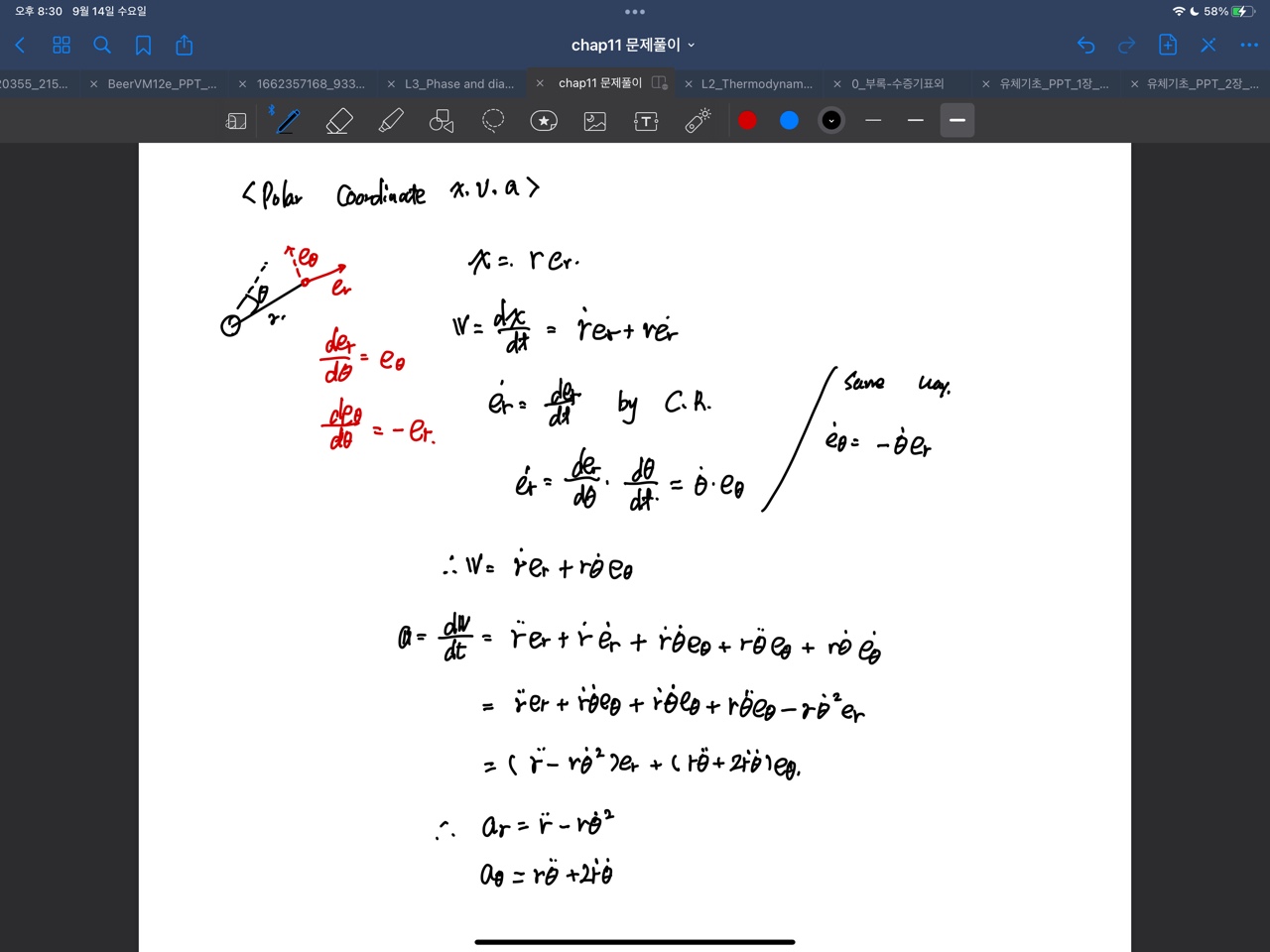
\[\vec{e_b} = \vec{e_t}\times \vec{e_n}\] \[\vec{e_b} : \text{binormal}\]

Polar Coordinate x, v, a

• Radial 방향과 theta가 커지는 방향을 각각 $\vec{e_r} ,\vec{e_\theta}$라고 하자.
• 삼각형을 그려 벡터의 뺄셈을 생각해 보면,

\[{d \vec{e_r} \over d\theta} = \vec{e_\theta}, {d\vec{e_\theta} \over d\theta} = -\vec{e_r}\] \[\boldsymbol{x} = r\vec{e_r}\] \[\boldsymbol{v} = {d\boldsymbol{x}\over dt} = \dot{r} \vec{e_r} + r\dot{e_r}\] \[\dot{e_r} = {d\vec{e_r} \over d \theta} {d\theta \over dt} = \dot{\theta} \cdot \vec{e_\theta}\] \[\therefore \boldsymbol{v} = \dot{r} \vec{e_r} + r\dot{\theta} \vec{e_\theta}\]

같은 방법으로,

\[\vec{a} = {d \vec{v} \over dt} = \ddot{r} \vec{e_r} + \dot{r} \dot{e_r} + \dot{r} \dot{\theta} \vec{e_\theta} + r\ddot{\theta} \vec{e_\theta} + r\dot{\theta} \dot{e_\theta}\] \[= \ddot{r} e_r + \dot{r}\dot{\theta} e_\theta + \dot{r} \dot{\theta} e_\theta + r\ddot{\theta}e_\theta - r{\dot{\theta} }^2 e_r \\ = (\ddot{r}-r{\dot{\theta } }^2 )e_r + (r\ddot{\theta}+2\dot{r}\dot{\theta}) e_\theta\]