[공수2] - Chap 9 벡터 미분

9.3 Curves

• Curve : 1개의 매개변수 t로 매개화 가능한 경우

Curve의 미분

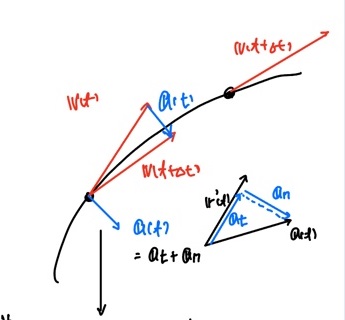
\[\boldsymbol{r'}(t) = \lim\limits_{\Delta t\rightarrow 0} {\boldsymbol r(t+\Delta t)-\boldsymbol r(t) \over \Delta t } \\ = \boldsymbol v(t) = (\lim\limits_{\Delta t\rightarrow 0} {\boldsymbol x(t+\Delta t)-\boldsymbol x(t) \over \Delta t }, \cdots, \cdots)\] \[\boldsymbol {v'}(t) = \boldsymbol r''(t) = \boldsymbol a(t) = \lim\limits_{\Delta t \rightarrow 0} {\boldsymbol v(t+\Delta t)-\boldsymbol v(t) \over \Delta t}\]

• a 의 방향 : 진행방향의 수직인 방향과 수평인 방향 성분으로 나뉨. (구심 가속도 생각해보기.)

  $\boldsymbol{a} = \boldsymbol{a}_n + \boldsymbol{a}_t$

  $\boldsymbol{a}_t = \text{proj }\boldsymbol{v}(\boldsymbol{a})$

  proj (정사영은 정의를 생각해보면, $\boldsymbol{a}$ 벡터 크기의 $cos $ 만큼의 크기를 $\boldsymbol{v}$ 방향 단위벡터에 곱한 것.)

\[proj_{\boldsymbol v} (\boldsymbol a) = \vert \boldsymbol a \vert \cos \gamma {\boldsymbol v \over \vert \boldsymbol v \vert} \\ \cos\gamma = {\boldsymbol a \cdot \boldsymbol v \over \vert \boldsymbol a \vert \vert \boldsymbol v \vert}\] \[\boldsymbol a_t = {\boldsymbol a \cdot \boldsymbol v \over {\vert \boldsymbol v \vert}^2} \boldsymbol v \\ \boldsymbol a_n = \boldsymbol a - \boldsymbol a_t = \boldsymbol a - {\boldsymbol a \cdot \boldsymbol v \over {\vert \boldsymbol v \vert}^2} \boldsymbol v\]

추가적으로, $v ^2 = v v $이므로, 내적을 이용하여 proj를 표현하는 것이 더 편할 수도 있다.

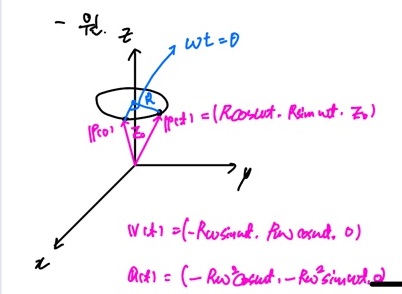
원

• Z좌표가 $z_0$이면서 $x-y$평면에 평행한 평면 위, 중심이 $(0, 0, z_0)$이고, 반지름이 $R$ 인 원을 생각하자.

  각속도는 $ω$

\[\boldsymbol v (t) = (-R\omega\sin{\omega t}, R\omega\cos{\omega t}, 0) \\ \boldsymbol a (t) - (R\omega^2\cos{\omega t}, -R\omega^2\sin{\omega t}, 0)\]

- 속도와 가속도의 크기

\[v=\vert \boldsymbol v(t) \vert = R\omega \\ a = \vert \boldsymbol a (t)\vert = R\omega ^2\] \[\omega = {v \over R}\]

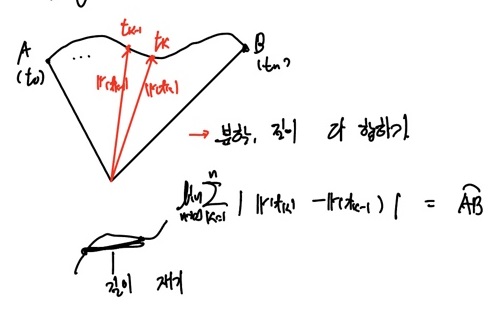
Length of curve

• 시점 $a = t_0$ 에서의 점 _A_와 시점 $b = t_n$ 에서의 점 $B$ 사이에서 매개변수 $t$의 구간 $[a, b]$ 를 $n$등분 하였을 때, $\overline{AB}$ 는 각각의 $n$등분된 선분의 길이의 합과 유사하다.

\[\lim\limits_{n\rightarrow \infty} \sum_{k=1}^n \vert \boldsymbol r(t_k)-\boldsymbol r(t_{k-1})\vert = \overline{AB}\]

• 중간값 정리에 의해

\[\boldsymbol r(t_k) - \boldsymbol r(t_{k-1}) = \boldsymbol r ' (c)(t_k - t_{k-1}) \\ t_{k-1} < c < t_k\] \[n \rightarrow \infty, t_k \approx c \\ \boldsymbol r(t_k) - \boldsymbol r(t_{k-1}) = \boldsymbol r' (t_k) (t_k-t_{k-1}) = \boldsymbol r' (t_k) \Delta t\] \[l = \lim\limits_{n\rightarrow \infty} \sum_{k=1}^n \vert \boldsymbol r' (t_k) (t_k - t_{k-1}) \vert\]

정적분의 정의에서 활용한 점을 이용하면, $t_k - t_{k-1} = {b-an} $, 즉 등간격이므로,

\[\lim\limits_{n\rightarrow \infty} \sum_{k=1}^n \vert \boldsymbol r' (t_k) ({b-a \over n})\vert \\= \int_a^b \vert \boldsymbol r'(t)\vert dt\]

• 위 식의 해석 :

  $r’(t) $ : 속력

  $dt $ : 시간

  속력 × 시간 = 길이 가 되어, 물리에서의 직관과 일치함을 알 수 있다.

호(arc), 길이로의 매개화

• 원의 일부 → 호 , 곡선의 일부 또한 호(arc)
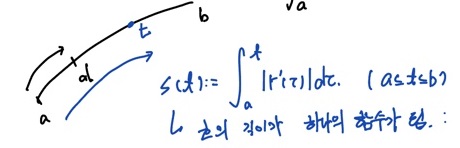
• arc의 길이 :

\[\int_a^b\vert \boldsymbol r'(t)\vert dt\]

• $t = a$ (시점)부터 $[a, b]$ 구간 내의 임의의 $t$에 대해 호의 길이 또한 하나의 함수가 됨, 또한 구간 내에서 함수는 멈추는 점이 없다면 ($

  \boldsymbol{r}’(t)

  \neq 0$) 증가함수이므로 매개변수 t에 대해 일대일대응이며 역함수가 존재함을 알 수 있다.

\[s(t) = \int_a^t|\boldsymbol{r}'(\tau)|d\tau\]

• 호의 길이가 하나의 함수가 됨 : arc length function

\[{d(s(t))\over dt} = \vert \boldsymbol r'(t)\vert = \boldsymbol v(t)\]

• 정적분의 기본정리에 의해 성립
• if$ \vert\boldsymbol{r}’(t)\vert \neq 0 (\boldsymbol{v}(t) \neq 0),$

\[{ds \over dt}>0\]

s : 증가함수, inverse exists


s : [_a_, _t_] → [0, _L_] : 증가함수.


by chain rule,

\[{d (\boldsymbol r (t) )\over ds } = {d (\boldsymbol r (t))\over dt} \cdot {dt \over ds} = {d (\boldsymbol r (t))\over dt} \cdot {1 \over {ds \over dt} } = {\boldsymbol r'(t) \over v(t)} = {\boldsymbol r'(t) \over \vert \boldsymbol r'(t) \vert }\]

Unit vector가 나옴을 알 수 있다. 이를 Unit tangent vector라 부름. 위치벡터를 길이에 대해 미분하면, 크기가 1인 속도벡터를 얻을 수 있다.

Curvature Vector

• Definition of curvature vector (u : unit tangent vector, s로 매개화, t로 매개화 상관 x)

  이 강의에서만 u 사용, T를 주로 사용

\[\boldsymbol \kappa(s) = {d(\boldsymbol u(s)) \over ds}\] \[\boldsymbol \kappa(s) = {d^2 r \over ds^2}\\ \vert \boldsymbol \kappa(s)\vert = \kappa (s) := \text{Curvature}\]

if $ r’(t) = 1 $, $\boldsymbol{\kappa} = \boldsymbol{r}''(t)$ (acceration vector)

Another derivation (parameteriaztion using t)

\[{ds \over dt} = \vert r'(t) \vert \ \ \ N(t) := {T'(t) \over \vert T'(t) \vert} \ \ \ \kappa(t) = \vert {dT \over ds}\vert\]

T : unit tangent vector, N : unit normal vector

by definition of curverture, and chain rule

\[{dT \over ds} = {dT \over dt} \cdot {dt \over ds} = {T' \over \vert r' \vert}\] \[\kappa(t) = \vert {dT \over ds}\vert = \vert{T'\over \vert r' \vert}\vert\]

한편, unit tangent vector의 정의에 의해

\[r'(t) = |r'(t)|T(t)\] \[r''(t) = {d r'(t) \over dt} = {d \vert r'(t) \vert \over dt} T(t) + \vert r'(t) \vert T'(t)\] \[= {d \vert r'(t) \vert \over dt} T(t) + \vert r'(t) \vert^2 \kappa(t) N(t)\] \[r''(t) \times r'(t) = \bigg({d \vert r'(t) \vert \over dt} T(t) + \vert r'(t) \vert^2 \kappa(t) N(t) \bigg) \times \vert r'(t) \vert T(t)\] \[= |r'(t)|3\kappa(t)(N(t) × T(t))\] \[|r''(t) × r'(t)| = |r'(t)|3κ(t)\] \[\therefore \kappa(t) = {\vert r''(t) \times r'(t) \vert \over \vert r'(t) \vert^3}\]

Reference

또다른 방법으로는, r(t) = cos θî + sin θĵ 로 두고,

$ddt $ 를 표현해 주는 방법으로도 증명 가능.

9.4 Fields

Scalar fields (다변수 함수)

• 공간상의 점 $P \in \R^3$가 $\R$ 로 대응됨.
• 일변수 함수에서의 미분의 정의

\[f'(x) = {dy \over dx} = {df \over dx}\]

• 다변수 함수에서라고 달라질까?, 동일함. but 편미분으로 정의됨 (Partial derivative)

\[{\partial f \over \partial x}, {\partial f \over \partial y}, {\partial f \over \partial z}\]

- 연속성이 보장되지는 않으나, (편)도함수가 연속이면 _f_는 일급 (_c_) 함수임.

Gradient

• 일변수 함수에서 $f(x)$의 도함수인 $f’(x)$가 존재한다. 동일한 방법으로 Scalar field에서의 각각의 변수에 대한 편도함수를 벡터로 나타낸 것이 gradient.

\[\nabla f := ({\partial f \over \partial x}, {\partial f \over \partial y},{\partial f \over \partial z})\]

• 일변수 함수에서의 합성함수의 미분은, chain rule을 따른다.

\[y=(f \cdot g) (x) \leftrightarrow y' = f'(g(x)) \cdot g(x) = {df \over du} \cdot {du \over dx} \ (g(x)=u)\] \[\{ f(\boldsymbol r(t)) \}' = {d(f(\boldsymbol r(t)))\over dt} = {\partial f(\boldsymbol r(t))\over \partial x}\cdot {dx \over dt} +{\partial f(\boldsymbol r(t))\over \partial y}\cdot {dy \over dt} +{\partial f(\boldsymbol r(t))\over \partial z}\cdot {dz \over dt} \\ = \nabla f(\boldsymbol r(t)) \cdot \boldsymbol r'(t)\]

• more precisely, let’s only consider $x$

\[{df(\boldsymbol r (t)) \over dt }\vert_x = \lim\limits_{h\rightarrow 0} {f(x(t+h)) - f(x(t))\over h}\] \[=\lim\limits_{h\rightarrow 0} {f(x(t)+x(t+h)-x(t)) - f(x(t))\over x(t+h)-x(t)} {x(t+h )- x(t) \over h}\] \[=\lim\limits_{H, h\rightarrow 0} {f(x(t)+H) - f(x(t))\over H} {x(t+h )- x(t) \over h}\] \[= f\big(x(r(t))\big) ⋅ x'(t)\]

• 맨 마지막 줄의 ⋅ 은 inner product임. 일변수 함수와 동일하나, 벡터 형태로 나타내므로 mult가 아닌 inner prod임을 주의

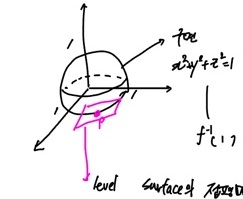
Gradient의 기하학적 의미

eg) $f(x, y, z) = x^2 + y^2 + z^2 $에서 구면은 f의 함수값이 같은 점들의 집합임.

반지름이 1인 구면 ($x^2+y^2+z^2=1, f^{-1}(1) $ : level surface (f의 1-등위면)

level surface위의 점 P의 접평면 (tangent plane)에 대한 법벡터 n = ∇f(P)

tangent plane 위의 arbitary point X, 평면의 방정식 :

∇f(P) ⋅ (X − P) = 0

9.5 Vector Field

• 벡터장, x,y,z에 대해 벡터가 대응되는것. 다변수 함수가 3개라고 생각해도 됨?
• P점에서의 vector field : P점에서 시작하는 Vector 대응시킴.

V(P) = [V_1(_P), V_2(_P), V_3(_P)]

(eg) 곡선에서 정의된 Vector field : tangent vector field. : Curve의 접벡터에 대응되는 Vector field

(eg) Normal vector field : 어떠한 surface위의 점의 tangent surface의 normal vector에 대응.

(eg) 전기력

• 점 P(x, y, z) : 전하량 1
• 점 P(x, y, z) : 전하량 Q

\[\boldsymbol E(P) = {(P-P_0) \over r} \cdot {kQ\over r^2} = k{Q\over r^3} (P-P_0) = k {Q (x-x_0, y-y_0, z-z_0) \over ((x-x_0)^2+(y-y_0)^2+(z-z_0)^2)^{3/2} }\]

Vector Field 의 미분

divergence

• divergence : Vector Field → Scalar Field

\[[v_1, v_2, v_3] = \boldsymbol v \rightarrow div\boldsymbol v = ({\partial v_1\over \partial x}+{\partial v_2\over \partial y}+{\partial v_3\over \partial z}) = \nabla \cdot \boldsymbol v\]

• Physical meaning of divergence

P점을 통과하는 유체의 질량 변화율과 관련이 있음.

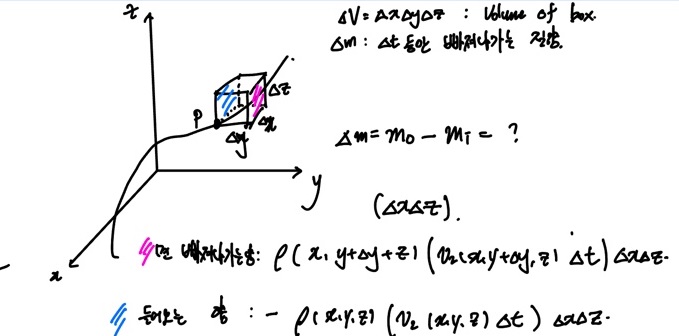
유선 : 공간상에서 유체의 속도 벡터를 이은 것이므로 curve임. 이 위의 점 P에 대해서 미소 길이 Δx, Δy, Δz_를 정의하고, _P(x, y, z)를 한 꼭짓점으로 하는 크기가 각각 dx, dy, dz인 정사각형을 고려하자.

ΔV = ΔxΔyΔz : Volume of the box

Δm = mo − mi : _Δt_의 시간 동안 빠져나가는 유체의 질량.

유체의 밀도를 ρ(x, y, z)라 하자.

• x-z Plane의 우측으로 빠져나가는 양

  mout, xz = ρ(x, y + Δy, z)(v_2(_x, y + Δy, z)Δt)ΔxΔz

• x-z Plane의 좌측으로 들어오는 양

\[m_{in,xz} = -(x,y,z) (v_2(x,y,z)t) x z\]

• 최종적으로 x-z Plane으로의 유출량

\[\Delta m_{xz} = {(\rho v_2)(x,y+\Delta y, z) - (\rho v_2)(x,y,z) \over \Delta y}\cdot \Delta t \Delta V\]

(_Δy_를 분자 분모에 곱하고 dV로 바꿈)

• $y $, P점에서의 x-z 방향의 순간질량변화율이므로, 이를 확장하면,

\[\Delta m=\{ {\partial (\rho v)\over \partial x}(P)+{\partial (\rho v)\over \partial y}(P)+{\partial (\rho v)\over \partial z}(P)\} \Delta t \Delta V\] \[{\Delta m \over \Delta t } \approx div(\rho \boldsymbol v)(P) \Delta V\] \[div(\rho \boldsymbol v) (P) \approx { {\Delta m \over \Delta t } \over \Delta V}\]

• 단위체적당 질량 변화율 (${\dot m \over \Delta V}$)

\[div (\rho \boldsymbol v) (P, t_0) = \lim\limits_{\Delta V \rightarrow 0} {\lim\limits_{\Delta t \rightarrow 0} {\Delta m \over \Delta t} \over \Delta V}\]

단위체적당 질량변화율 _Δm_/_Δt_ = _ṁ_:= _flux_

• 한편,

  m(t_0) = _ρ(P, t_0)_ΔV

  m(t_0 + _Δt) = ρ(P, t_0 + _Δt)ΔV

  m(t_0 + _Δt) − m(t_0) = _mi − mo

  질량 변화량 = - 질량 유출량

  mo − mi = −(ρ(P, t_0 + _Δt) − ρ(P, t_0))_ΔV ≈ Δm

• 이를 div로 정리된 식에 대입 하면,

\[div(\rho \boldsymbol v) (P) = \lim\limits_{\Delta t \rightarrow 0} {\rho (P, t_0+\Delta t)-\rho (P,t_0) \over \Delta t} = -{\partial \rho (P, t_0)\over \partial t}\]

• Reynolds Transport Theorem (a.k.a. Mass conversion law) , simplified

\[div(\rho \boldsymbol v) + {\partial \rho \over \partial t} = 0\]

Laplacian

• Gradient : Scalar Field → Vector Field.
• Divergence : Vector Field → Scalar Field
• Laplacian : Scalar Field → Vector Field → Scalar Field

\[f \rightarrow \nabla f \rightarrow div(\nabla f) = \nabla^2 f \\ = {\partial^2f \over \partial x^2}+{\partial^2f \over \partial y^2}+{\partial^2f \over \partial z^2}\]

Curl

• curl : Vector Field → Vector field

\[\boldsymbol v = (v_1, v_2, v_3) \rightarrow curl \boldsymbol v := \nabla \times \boldsymbol v \\ = ({\partial v_3 \over \partial y}-{\partial v_2 \over \partial z}, {\partial v_1 \over \partial z}-{\partial v_3 \over \partial x}, {\partial v_2 \over \partial x}-{\partial v_1 \over \partial y})\]

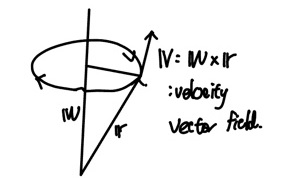
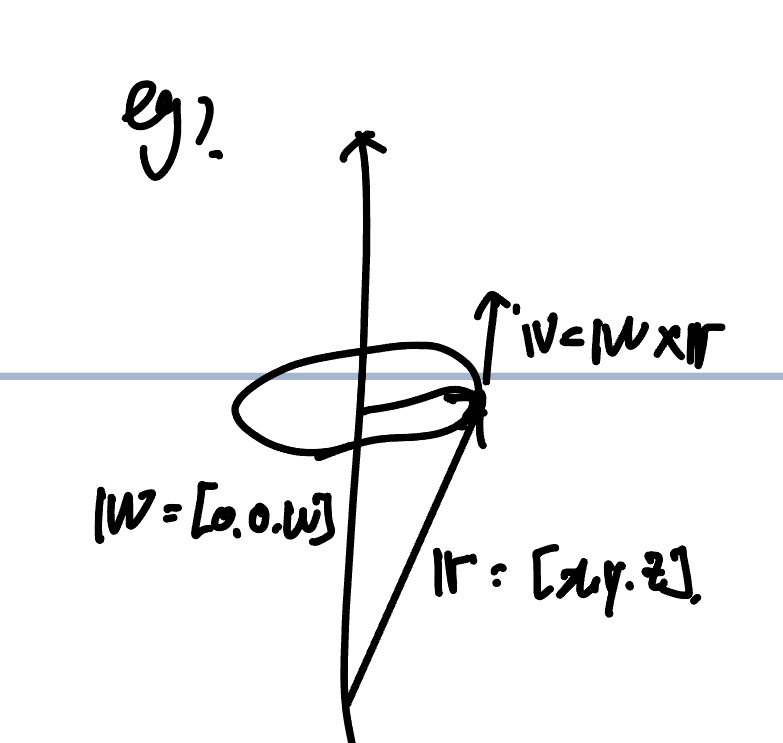
(eg) ω = (0, 0, ω) 로 회전하는 경우를 고려해보자.

\[\boldsymbol r = (x,y,z) \\ \boldsymbol v = \boldsymbol \omega \times \boldsymbol r = [0,0,\omega] \times [x,y,z]\]

curl v = curl(ω × r) = curl([−ωy, ωx, 0]) = [0, 0, 2ω]

• 유체의 회전은 ${1 \over 2} \cdot curl \boldsymbol v$ 로 나타낼 수 있음을 알 수 있다.

Proposition rule in vector calculation

1. curl (∇f) = ∇ × ∇f = 0
2. div(curl v) = 0
   • consider triple product rule of vector