[공수2] - Chap 10. 벡터 적분

Chap 10. Vector integral & Calcalus

10.1 Line integrals

• 기본적으로 t로 매개화된 곡선을 따라 Vector Field 적분하는 것.

(eg) 곡선 r(t)를 따라 힘 F를 적분해 보자.

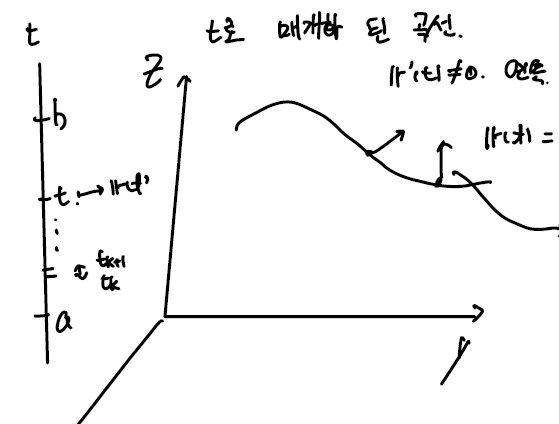
• t로 매개화 된 곡선

t → r(t) = [x(t), y(t), z(t)] (a ≤ t ≤ b)

• 각 r(t)의 점 마다 힘(Vector Field) F(r(t)) = [_F_1, _F_2, _F_3]
• Curve C를 따라 F라는 힘을 적분하여 할 수 있는 일의 양을 계산해 보자.
• 구간 t ∈ [a, b]를 n개의 등간격으로 분할해 보자.

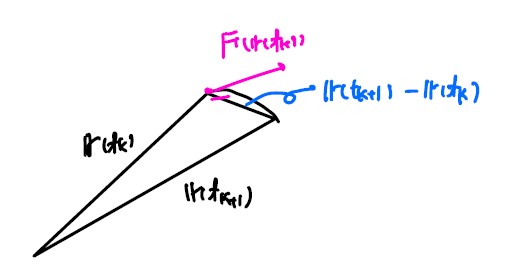
이 때 인접한 tk, tk + 1에 대하여,

$w_k := F(r(t_k)) ⋅ (r(t_{k + 1}) − r(t_k))$

중간값 정리에 의해

$r(t_{k + 1}) − r(t_k) ≈ r’(t_k)(t_{k + 1} − t_k)$

정적분의 정의에 의해

\[W = \lim\limits_{n\rightarrow \infty} \sum_{k=1}^n w_k = \int_a^b \boldsymbol F(\boldsymbol r(t)) \cdot \boldsymbol r'(t) dt := \int_C \boldsymbol F(\boldsymbol r) \cdot d\boldsymbol r\]

또한 이렇게도 표기할 수 있다.

Physically, r′(t) 는 speed임.

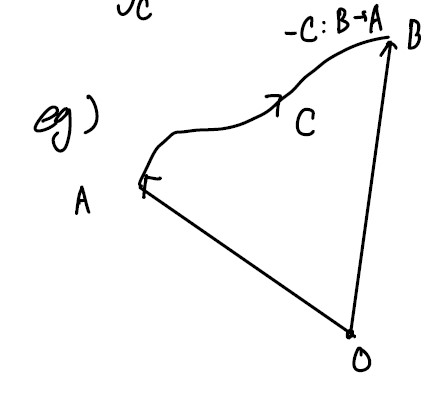
\[W = \int F \cdot ds = \int F \cdot {ds \over dt} dt = \int F \cdot v dt\] \[\begin{aligned} \int_C \boldsymbol F(\boldsymbol r) \cdot d\boldsymbol r &= \int_a^b \boldsymbol F(\boldsymbol r(t)) \cdot \boldsymbol r'(t)dt \\ &= \int_a^b \bigg(F_1\big(\boldsymbol r(t)\big){d x\over d t}+F_2\big(\boldsymbol r(t)\big){d y\over d t}+F_3\big(\boldsymbol r(t)\big){d z\over d t}\bigg) \\ &= \int_C F_1 dx+F_2 dy + F_3 dz \end{aligned}\]

힘의 적분에서 경로를 반대로 잡을 경우, 다음과 같음을 알 수 있다.

\[C : A \rightarrow B \\ -C : B \rightarrow A\]

r(t) (a ≤ t ≤ b) ↔︎ r(a + b − t) (a ≤ t ≤ b)

\[\begin{aligned}\int_{-C} F(r(t)) ⋅ dr &= \int_a^bF(r(a + b − t))(−1) ⋅ r′(a + b − t)dt \\ &= \int_b^aF(r(a + b − t)) ⋅ r′(a + b − t)dt \end{aligned}\] \[let \ u:=a+b-t \\ W = \int_a^b \boldsymbol F(\boldsymbol r (u))\cdot \boldsymbol r(u) (-1) du\]

(u로 치환하면서 적분범위 바뀌고, du = −_dt_에 의해 부호 한번 더 바뀜.)

\[= −\int_a^bF(r(t)) ⋅ r'(t)dt = −\int_CF(r) ⋅ dr\]

Conservative Vector Field

• 경로에 관계 없이 같은 시점과 종점에 대해 적분해 주었을 때 같은 값이 나오는 경우를 보존장(conservative vector field)라고 하며, 위의 예시 또한 보존장이다.

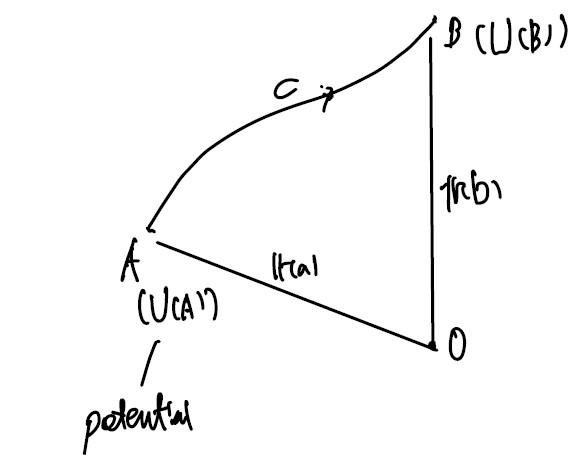
• 이 때 $\R$의 점에 대해 potential에 대응 되는 U(P) Scalar Field를 만들어줄 수 있는데,

  3

\[W_{a → b }= \int_a^bF(r) ⋅ dr = U(B) − U(A)\]

U를 F에 대한 부정적분처럼 볼 수 있으므로 다음과 같이 쓸 수 있다.

\[= \int_a^b {d \over dt} (U(\boldsymbol r (t)))dt = \int _a ^b (\nabla U)(\boldsymbol r(t)) \cdot \boldsymbol r'(t) dt\]

(위 줄은 합성함수의 미분을 생각하면 자명)

(eg) 돌이 B -> A로 떨어질 때 작용한 힘을 $F $ 라고 하면,

\[\int_{-C}-(r) ⋅ dr = −\int_CF(r) ⋅ dr = −\int_a^bF(r(t)) ⋅ r'(t)dt\]

F = −∇U

즉 Potential Energy가 감소하는 방향으로 중력이 작용함을 알 수 있으며, 이 때의 F를 보존력, conservative Force라 한다.

F : Conservative Vector Field $F =f $ (f : potential function of $F $)

(eg) $P_0$에 질량 M인 물체 A가 위치 할 때 $P$점에 질량 m인 물체 B의 포텐셜

\[\boldsymbol F(\boldsymbol r ) = -{c \over r^3} d\boldsymbol r = \nabla({c\over r})\]

에서 $c\over r$이 Potential Energy가 됨을 알 수 있다.

Theorem 1. Path independence

for F = ∇f, arbitary Curve C : A → B

\[\int_C\nabla f(r) ⋅ dr = \int_a^b \nabla f(r(t)) ⋅ r'(t)dt\] \[= \int_a^b {d\over dt} \bigg(f\big(\boldsymbol r (t)\big)\bigg)dt = f(\boldsymbol r(b))-f(\boldsymbol r(a)) = f(B)-f(A)\]

C의 시점과 종점의 위치만이 적분값에 영향을 주는 것을 알 수 있다.

In particular,

∮C : Closed

∇f(r(t)) ⋅ r′(t)dt = 0

시점과 종점이 같은 경우, 즉 C가 Closed Curve인 경우 적분값이 0임을 알 수 있다.

Theorem 2. Conservative -> curl F = 0

F = [F_1, _F_2, _F_3] = ∇_f ⇒ curl F = ∇ × ∇f = 0

(if _F_1, _F_2, _F_3의 편도함수가 연속)

역은 성립하지 않음.

(eg)

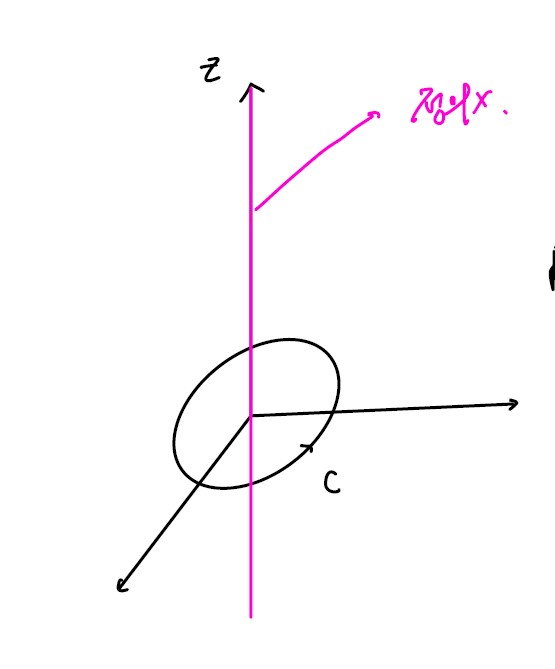
\[\boldsymbol F = {[-y,x,0] \over x^2+y^2}\]

undefined when x = 0, y = 0 (on z axis)

curl F = 0

but if C : circle on x-y plane centered at (0,0,0) counterclockwise

\[\int_C \boldsymbol F(\boldsymbol r) \cdot d\boldsymbol r = \int_C {-ydx+xdy\over x^2+y^2}\]

$ y=, x = $ 대입하면,

\[= \int_0^{2\pi} {(-\sin\theta)(-\sin\theta)+\cos\theta\cos\theta\over 1}d\theta = 2\pi \neq 0\]

F 가 정의되지 않는 선을 포함하도록 Curve를 잡을 경우 curl F = 0이지만, 폐곡선을 따라 적분한 potential이 0이 되지 않음을 알 수 있다.

10.2 Green’s theorem

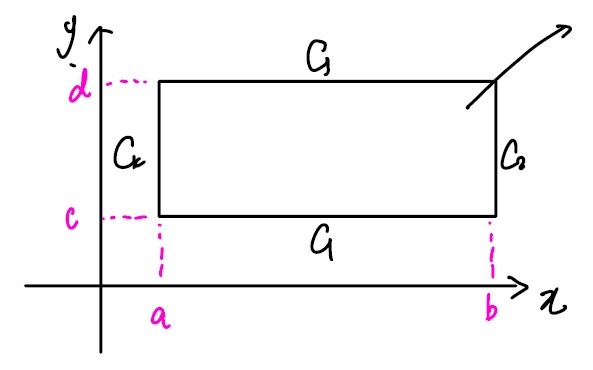
x-y평면의 2차원을 먼저 생각해 보자.

(a, c), (b, c), (b, d), (a, d) 4개의 점을 잇는 선분으로 만든 Closed Curve를 고려하자.

Rectangle 내부의 Vector Field F = (P(x, y), Q(x, y))

$C = R $ : Boundary of C

= _C_1 ∪ _C_2 ∪ _C_3 ∪ _C_4 (smooth curve) : Finite smooth curves

\[∮_CPdx + Qdy = ∮_CF(r)dr = ∑i∫_CiF(r)dr\]

(C를 따라 F를 선적분함.)

for i=1, y = c_로 고정이고, _x = a → b 이므로,

r(x) = [x, c] (a ≤ x ≤ b)

이면, r′(x) = [1, 0]

\[∫_{C_1}F(r)dr = ∫_a^b[P(x, c), Q(x, c)] ⋅ [1, 0]dx = ∫_a^bP(x, c)dx\]

같은 방법으로 i = 2, 3, 4에 대해서도 진행.

단, r′(t) 음수 일 수 도 있음. 방향에 따라

combining w/ P, Q :

\[\oint_C Pdx + Qdy = \int_c^d (Q(b,y)-Q(a,y))dy - \int_a^b (P(x,d)-P(x,c))dx \\ \int_c^d \int_a^b{\partial Q \over \partial x}(x,y) dx \cdot dy - \int_a^b \int_c^d {\partial P \over \partial y} (x,y) dy \cdot dx\]

라이프니츠법칙?에 의해 $\partial P \over \partial y$ 가 연속이므로, 적분 순서 바꾸어도 됨.

\[= \int_c^d \int_a^b ({\partial Q \over \partial x}-{\partial P \over \partial y}) dx dy =: \int\int_R ({\partial Q \over \partial x}-{\partial P \over \partial y}) dx dy\] \[\therefore \oint_C Pdx + Qdy = \int\int_R ({\partial Q \over \partial x}-{\partial P \over \partial y}) dx dy\]

assumption : ${\partial P \over \partial y} , {\partial Q \over \partial x}$가 continuous

Theorem 1. Green’s Theorem

for closed region R in $\R^2$

$ C = R $ C : contour of R, finite number of smooth curves

\[\int_{\partial R} Pdx + Qdy = \int\int_R ({\partial Q \over \partial x}-{\partial P \over \partial y}) dx dy\]

단, assumption : ${\partial P \over \partial y} , {\partial Q \over \partial x}$가 continuous

(eg) C : 단위원, F(x, y) = [y_2 − 7_y, 2xy + 2x]

\[∮_CF(r)dr = ∮_C(y2 − 7y)dx + (2xy + 2x)dy = ∫∫_D((2x + 2) − (2y − 7))dxdy = 9∫∫_Ddxdy = 9π\]

10.3 Surface Integral

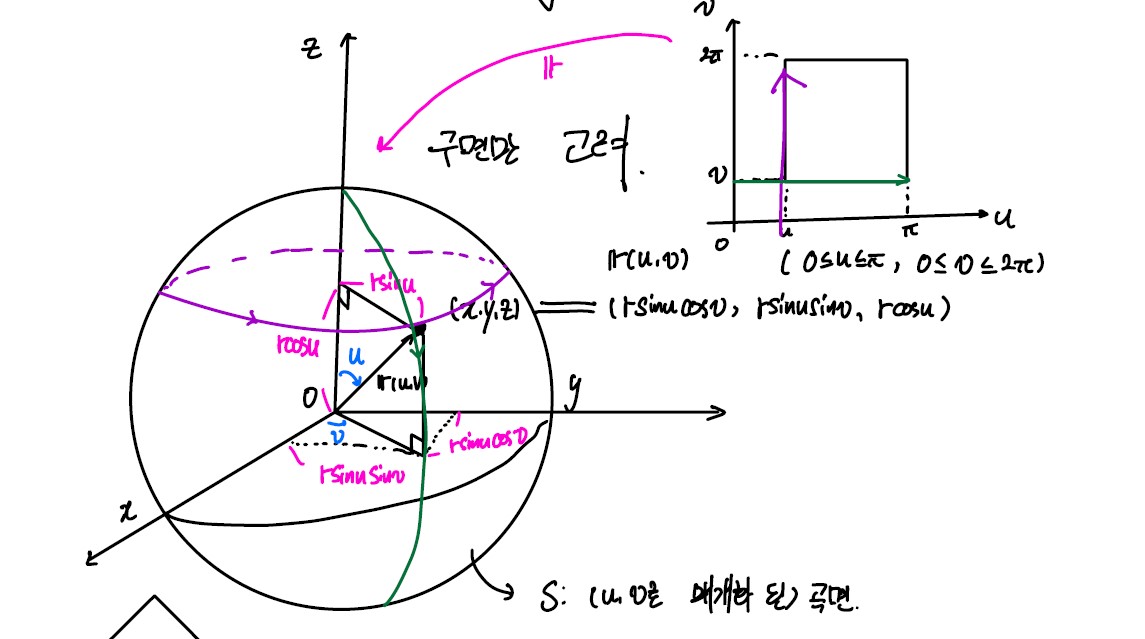
구면 : 2개의 parameter로 매개화 해보자. u,v

P(x, y, z) = (r_sin _u_cos _v, r_sin _u_sin _v, r_cos _u)

S : (u,v)로 매개화 된 곡면

\[\boldsymbol r_v (u,v) = [-r\sin u \sin v,\ r \sin u \cos v, \ 0], \\ \boldsymbol r_u (u,v) = [r \cos u \cos v, \ r \cos u \sin v ,\ -r\sin u]\]

($r_u $ : u가 변수, v를 고정시켰다는 의미)

From now on, consider only rv × ru ≠ 0

rv × ru 연속인 곡면

S : orientable surface

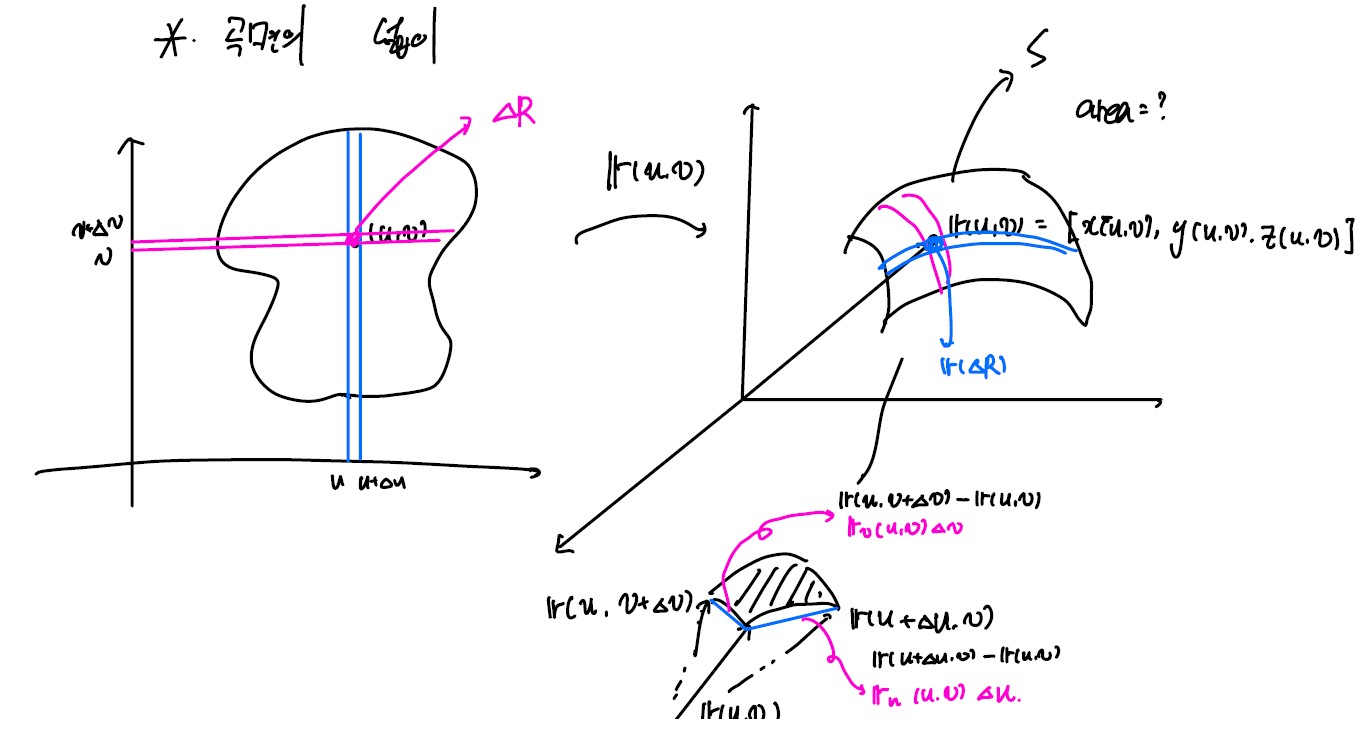
곡면의 넓이

u,v 평면에서, [u, u + Δu], [v, v + Δv] 범위의 작은 사각형에 대한 실제 곡면의 넓이

실제 곡면에서는 r(u, v), r(u + Δu, v), r(u, v + Δv), r(u + Δu, v + Δv) 의 4개의 꼭짓점을 가진 사각형 형태의 곡면에 대응됨.

각 꼭짓점을 직선으로 연결하는 벡터를 만들어보자.

(위의 정의에 의해)

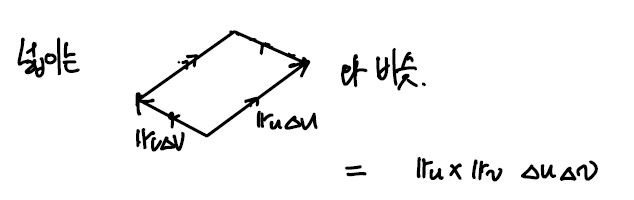
\[\boldsymbol r(u,v+\Delta v) - \boldsymbol r(u, v) = \boldsymbol r_v(u,v)\Delta v \\ \boldsymbol r(u+\Delta u, v) - \boldsymbol r(u,v) = \boldsymbol r_u (u,v)\Delta u\]

이 때 넓이는 외적의 정의에 의해 두 벡터의 cross product와 유사함.

ΔR = ru × rvΔvΔu

\[Area(S) = \int\int dA \\ = \lim_{\Delta u,\Delta v\rightarrow 0} \sum \vert \boldsymbol r_u \times \boldsymbol r_v \vert \Delta u \Delta v = \int\int_R \vert \boldsymbol r_u \times \boldsymbol r_v \vert dudv\]

while $ dudv = dA$, element of area over S (S의 면적소)

(eg) S : r(u, v) = [r_sin _u_cos _v, r_sin _u_sin _v, r_cos _u] , (0 ≤ u ≤ π, 0 ≤ v ≤ 2π)

dA =

ru × rv

dudv = r_2sin _ududv

area(S) = ∫02π∫0πr_2sin _ududv = ∫02π_2_r_2_dv = 4_πr_2

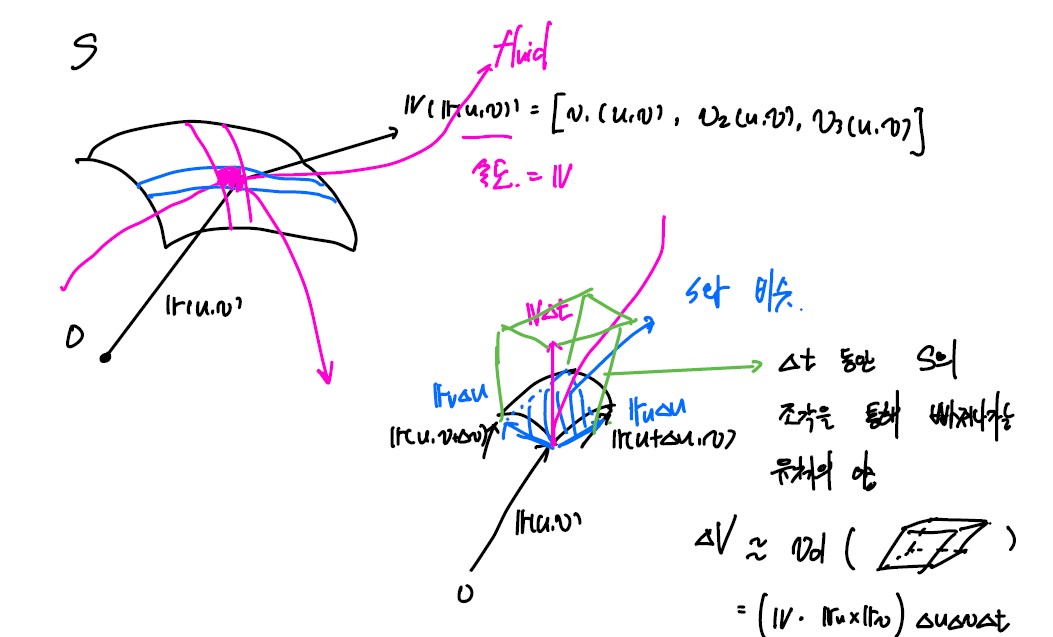
곡면에서의 벡터장의 적분

유체의 예시에서, v(r(u, v)) 는 r(u, v)에서의 유체의 속력을 벡터로 나타낸 함수.

이 때 특정 곡면을 빠져나가는(통과하는) 유체의 양을 계산하기 위해 곡면 위에서의 속도 벡터장을 적분해보자.

해당 면적소의 면적 $$ 그 위치에서의 속력 × Δt = $t $ 동안 S의 조각을 통해 빠져나가는 유체의 양.

ΔV ≈ v ⋅ (ru × rv)ΔuΔvΔt

\[{\Delta V \over \Delta t} \approx \boldsymbol v \cdot (\boldsymbol r_u \times \boldsymbol r_v) \Delta u \Delta v\]

S를 통해 빠져나가는 유체의 양의 순간변화율.

여기서 분자와 분모에 각각 두 방향벡터의 외적의 절댓값을 곱고 나누어 처리해주면,

\[= \int\int_R \boldsymbol v \cdot {\boldsymbol r_u \times \boldsymbol r_v \over \vert \boldsymbol r_u \times \boldsymbol r_v \vert \cdot \vert \boldsymbol r_u \times \boldsymbol r_v \vert dudv} \\ = \int\int_R \boldsymbol v \cdot \boldsymbol n dA\]

Surface Integral :

∫∫Rv ⋅ ndA := ∫∫Rv ⋅ n(r(u, v))dA

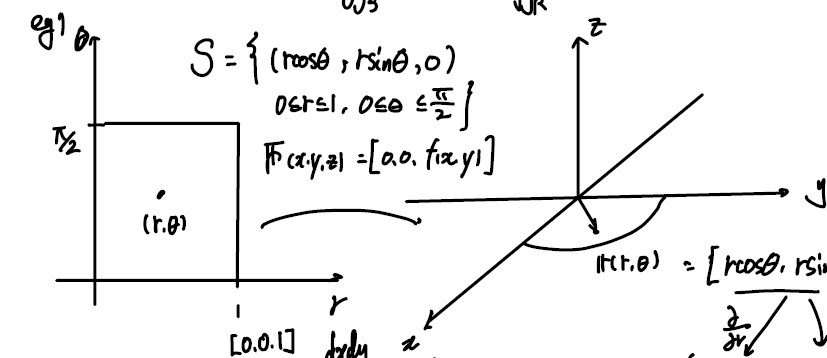
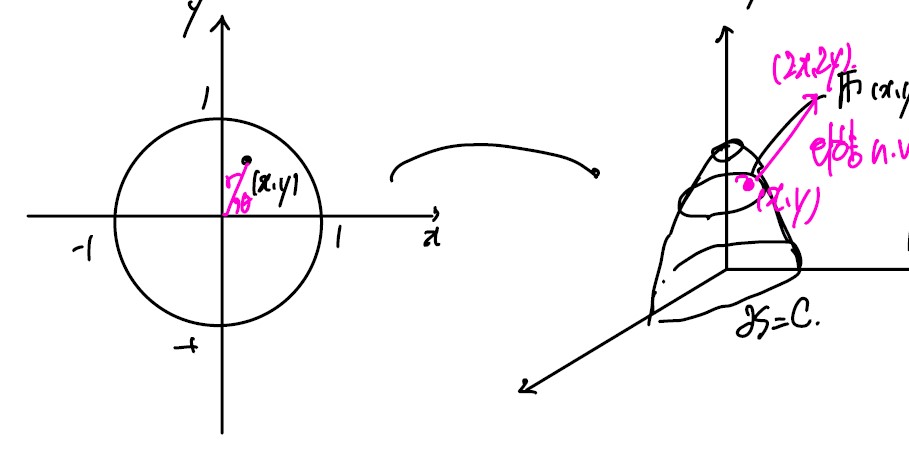
(eg) $S = {(r\cos\theta, r\sin\theta, 0) \ 0\leq r\leq 1, 0 \leq \theta \leq {\pi \over 2} }$

F(x, y, z) = [0, 0, f(x, y)]

n = [0, 0, 1], dA = dxdy

(수학2에서 배운 변수 바꾸는거 생각하면 됨)

\[\int\int_S \boldsymbol F \cdot \boldsymbol n dA = \int\int_R \boldsymbol F \cdot (\boldsymbol r_r \times \boldsymbol r_\theta) dr d\theta \\ = \int\int_S[0,0,f(r\cos\theta, r\sin\theta)] \cdot ([\cos\theta, \sin\theta, 0]\times [-r\sin\theta, r\cos\theta, 0]) dr d\theta\]

= ∫∫Rf(r_cos _θ, r_sin _θ) ⋅ rdrdθ

(Transformation from cartesian to polar coordinate)

10.4 Divergence Theorem

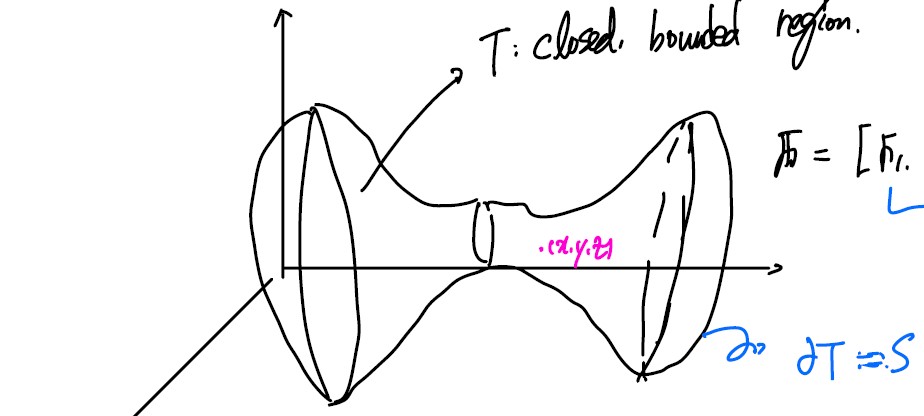
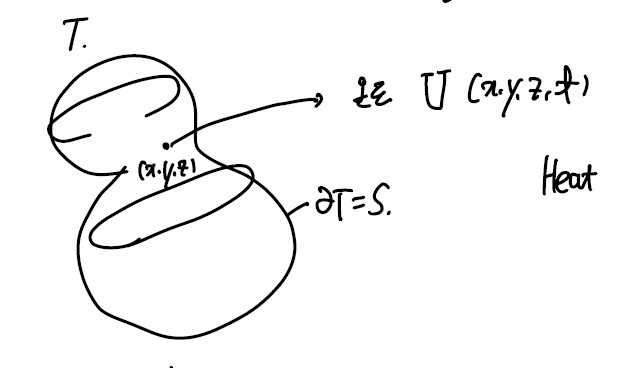
T : closed, bounded region.

$F = [F1, F2, F3] $ : continuous

F의 편도함수들이 연속.

∂T = S : Piecewise smooth orientable surface

Divergence Theorem :

∫∫∫TdivFdxdydz = ∫∫SF⋅ndA

\[div \boldsymbol F = {\partial F_1\over \partial x}+ {\partial F_2\over \partial y}+ {\partial F_3\over \partial z}\]

Proof ) (Roughly, 엄밀한 증명은 어려움)

∫∫SF ⋅ ndA = ∫∫S[F_1, _F_2, _F_3] ⋅ [n ⋅ _î, n ⋅ ĵ, n ⋅ k̂]dA

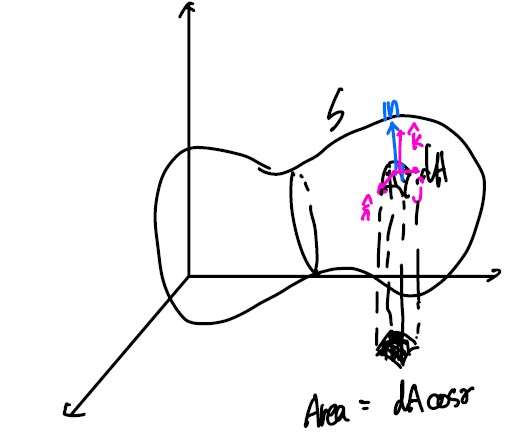
α = ∠(n, î), β = ∠(n, ĵ), γ = ∠(n, k̂)

위 식 =

\[{\int \int }_S F_1 (dA\cos\alpha)+ F_2(dA\cos\beta) + F_3 (dA\cos\gamma) \\ {\int \int} _S F_1 dydz + F_2 dxdz + F_3 dxdy\]

(xy평면에 떨어진 미소영역의 그림자(정사영)은 _dA_cos _γ_임. 같은 방법으로.)

also,

\[F_i = ({\partial \over \partial x_j}) (\int F_i dx_j)\] \[= {\int\int\int}_T ({\partial F_1\over \partial x}+ {\partial F_2\over \partial y}+ {\partial F_3\over \partial z}) dxdydz \\ = {\int\int\int}_T div \boldsymbol F dxdydz\]

(eg)

S : x_2 + _y_2 + _z_2 = 4, F = [7_x, 0, −z]

\[{\int\int}_S \boldsymbol F \cdot \boldsymbol n dA \\ = {\int\int\int}_B (7-1) dxdydz = 6 \times {4\over 3} \pi\times 2^3 = 64\pi\]

10.5 Heat Equation

3차원 공간 내 (x,y,z)에 온도 U(x,y,z,t)

T_라는 폐공간에서의 surface ∂_T

Heat Flow 의 속도 v ∝ ∇_U_이므로, 다음과 같이 모델링할 수 있다.

v = −k∇U

k : postive constant, -부호 : 시간이 지남에 따라 온도는 감소하므로.

H(t) : 시각 t에서의 T에 있는 열의 총량

H(t + Δt) ≈ H(t) − ∫∫Sv ⋅ ndAΔt

• 위 식의 integral : S를 통해 빠져나가는 heat의 순간 변화율 ×Δt

∇H(t) = −∫∫Sv ⋅ ndA = −∫∫∫Tdivvdxdydz = −∫∫∫T∇ ⋅ (−k∇U)dxdydz = −∫∫∫T − k∇2Udxdydz = ∫∫∫Tk∇2Udxdydz

\[\therefore {\partial H \over \partial t} = {\int\int\int}_T k \nabla^2 U dxdydz\]

Another way :

• assume that specific heat σ and density ρ are constant.

\[{\partial \over \partial t} {\int\int\int}_T \sigma(비열)U(온도)\times \rho dx dy dz(질량) = {\int\int\int}_T \sigma \rho {\partial U \over \partial t} dx dy dz\]

= ∫∫∫Tk∇2Udxdydz

두 식으로부터,

\[k\nabla^2U = \rho\sigma {\partial U \over \partial t}\]

U의 시간미분을 _Ut_라고하면,

\[U_t = {k\over \rho \sigma} \nabla^2 U = C^2\nabla^2 U\]

k, σ, ρ 모두 양수이므로, _C_2의 constant로바꾸어 주고 이를 Heat equation이라 한다.

10.6 Stoke’s Theorem

• 평면을 곡면으로 확장.
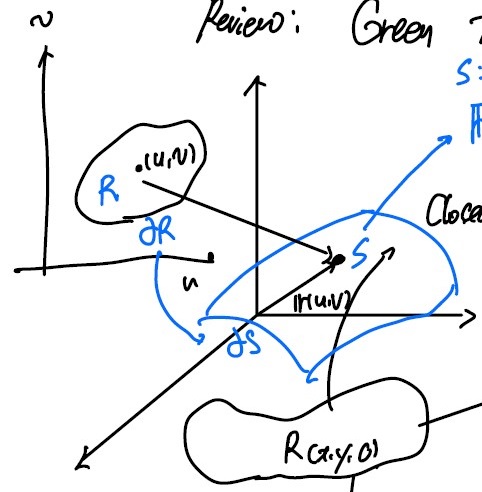
• Review : Green Theorem

v, u를 축으로 하는 2차원내의 폐곡선 내부 R, 테두리를 ∂R

이라 하면, v, u를 매개로 하는 곡면 S에 대해 테두리 ∂S

이 3차원 공간에서 정의되는 벡터장 F = [F1, F2, F3]

$S $ : piecewise smooth simple closed curve

z=0인, 곡면 S의 정사영인 _Rz_를 생각해보자. 여기서 Green’s Theorem을 사용하면,

F(x, y, 0) = [F1(x, y, 0), F2(x, y, 0), 0]

\[curl\boldsymbol F = [0,0,{\partial \boldsymbol F_2 \over \partial x} - {\partial \boldsymbol F_1 \over \partial y}]\] \[\oint \boldsymbol F (\boldsymbol r) d\boldsymbol r = \oint_R F_1dx + F_2dy = {\int\int}_R {\partial \boldsymbol F_2 \over \partial x} - {\partial \boldsymbol F_1 \over \partial y} dx dy \\ = {\int\int}_R curl\boldsymbol F \cdot \hat k dxdy\]

같은 방법으로 나머지 2개 차원에 대해 해주면 됨.

∮∂SF(r)dr = ∫∫ScurlF⋅ndA

Stoke’s theorem

(eg) S : z = 1 − (x_2 + _y_2), (_x_2 + _y_2 ≤ 1), F = [_y, z, x]

then, curlF = [−1, −1, −1]

r(x, y) = [x, y, 1 − (_x_2 + _y_2)]

\[\oint \boldsymbol F (\boldsymbol r)d \boldsymbol r = {\int\int}_S curl \boldsymbol F \cdot \boldsymbol n dA = {\int\int}_R curl \boldsymbol F (\boldsymbol r(x,y)) \cdot (\boldsymbol r_x \times \boldsymbol r_y) dxdy = {\int\int}_R [-1,-1,-1]\cdot [1,0,-2x]\times [0,1,-2y] dxdy \\ = {\int\int}_R (-2(x+y)-1)dxdy= {\int\int}_R (-2r(\cos \theta +\sin \theta)-1) r dr d\theta = -\pi\]

APplication of Stoke’s Theorem

• For a continuous vector field,

$ F = [F_1, F_2 , F_3]$

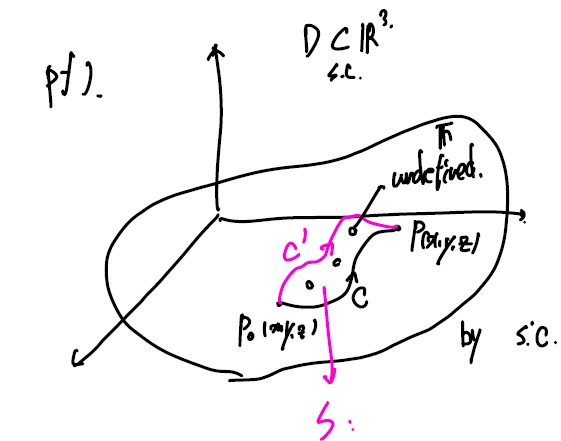
• simply connected : 영역 내 모든 curve를 연속적으로 움직여 D(arbitary point)로 shrink 가능

eg) $\R^3, \R^3 \backslash {0,0,0}$ : simply connected / $^3 {z-축} $ : X

$ curl F = F = f $

C : P_0 → _P, C′ : P → _P_0

∂S = C − C′

by Stoke’s Theorem,

∮C − C′F(r) ⋅ dr = ∫∫ScurlF ⋅ ndA = 0

즉 regardless of path, 시작점과 끝점이 정해지면 상태함수처럼 벡터를 따라 적분한 값이 동일함.

∫CF(r)dr = ∫C′F(r)dr

즉 퍼텐셜 함수 f(x,y,z)를 정의 가능

f(x, y, z) := ∫P_0(_x, y, z)F(r)dr

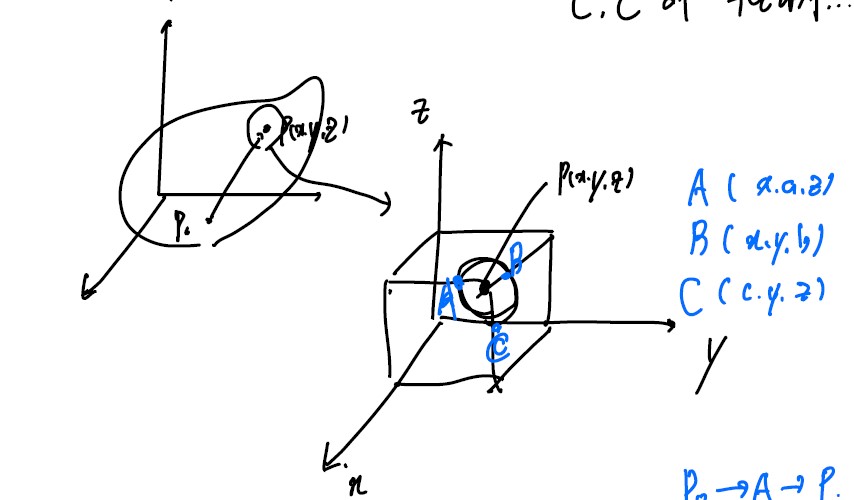
P점(종점) 주위로 cube를 생각해보자. $ A(x,a,z), B(x,y,b), C(c,y,z)$

_P_0에서 P로 가는 경로에서 A를 들러도, B를 들러도, C를 들러도 그 값은 같음.

f(x, y, z) = ∫P_0(_x, y, z)F(r)dr = ∫P_0_AF(r)dr + ∫A(x, y, z)F(r)dr

A → _P_에서, $ r(t) = (x,t,z) (aty)$ 이므로, 이를 적용해주면,

∫A(x, y, z)F(r)dr = ∫ayF(r(t)) ⋅ r′(t)dt = ∫ayF ⋅ [0, 1, 0]dt

= ∫ayF_2(_x, t, z)dt

여기서 f의 y로의 편미분을 생각해보면,

\[{\partial f \over \partial y} = {\partial \over \partial y} \int (constant) + {\partial \over \partial y} \int_a^y F_2 (x,t,z)dt = {\partial f \over \partial y} (x,y, z) = F_2(x,y,z)\]

∴ ∇f = [_F_1, _F_2, _F_3] = F

Stoke’s Theorem을 이용하여 Conservative vector field에서 Potential함수의 미분이 vector field임을 알 수 있다.