[C++] 오목 게임 구현
PM_Project 1
서론
열심히 구현해놓고 점수 만점까지 받았지만,, 헛수고가 되어버린..
C++ 오목 게임 만들기 입니다. 공개 repository로 전환해놨으니
필요하신분들은 열람하거나 fork 하셔도 됩니다.
REPOS : LINK
1. Introduction
1.1 이론적 배경
1.1.1 Omok game
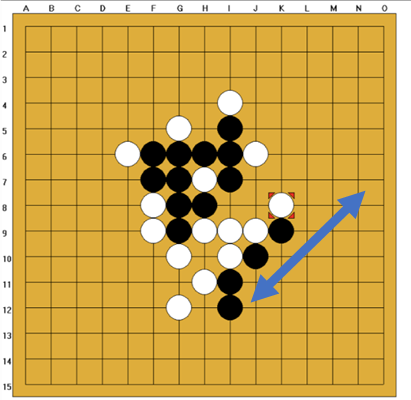
오목은, 2명의 플레이어가 번갈아가며 바둑판에 돌을 놓아, 자신의 말을 수직, 수평 혹은 대각선으로 5개 연속으로 놓을 경우 승리하는 게임이다.
[그림 1] 백이 대각선으로 5개를 놓아 승리한 모습
1.1.2 금수(3-3 rule) 1
일반적으로 아무 제약조건 없이 오목을 둘 경우 첫 수를 두는 (일반적으로 흑)이 압도적으로 유리하므로, 선공인 흑이 특정 자리에 두는 것을 막는 금수를 적용하게 된다. 일반적으로 3-3 이라고 불리는 자리에 놓을 수 없는 규칙이다. 이를 설명하기 위해서는 2가지 정도의 개념을 알아야 하는데, 먼저 오목에서 사용되는 용어 중 ’3’과 ’4’의 정의가 일반적인 3-in-a-row와 다름을 알아야 한다.
오목에서의 ‘3’은 현재 놓을 자리를 포함하여 2개의 돌을 놓았을 때 ‘open 4’를 만들 수 있는 자리를 ‘3’이라 한다. 같은 맥락으로 ‘4’는 현재 놓을 자리를 이용하여 2개의 돌을 놓았을 때 5-in-a-row를 만들어 게임을 승리하게 될 경우를 ‘4’라고 한다. 한편, ‘open 4’는 한 개의 돌을 추가하여 양쪽이 막혀 있지 않은, 즉 다른 색의 돌이나 판의 경계에 의해 가로막혀 있지 않은 ‘4’를 만들 수 있을 때의 상황을 open 4라고 한다. 추가적으로, 하나의 돌을 착수하여 ‘3’, ’4’를 동시에 만들 수 있는 경우는 ’4’라고 볼 수 있다. 이러한 맥락에서 ’3-3’은 하나의 돌을 착수하여 2개 이상의 ’3’을 만드는 경우, ’3-4’는 하나의 ’3’과 하나의 ’4’를 만드는 경우, ’4-4’는 두개 이상의 ’4’를 만드는 경우를 의미한다. 이 때 하나의 돌로 2개 이상의 ’3’을 만드는 수를 흑돌에서 놓을 수 없다.
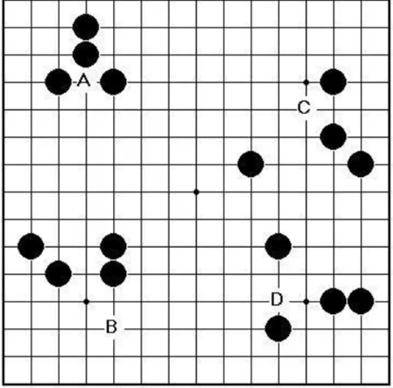
[그림 2] ‘3-3’ 금수인 경우의 예시
[그림 2]에서 A, B, C, D 모두 흑이 3-3인 자리로, 해당 자리에 착수했다고 가정하고 한 칸의 공백까지는 연결된 자리로 본다는 것을 알 수 있다.
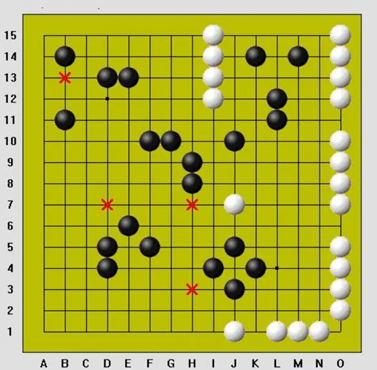
[그림 3] ‘3-3’ 이 아닌, 헷갈리는 경우의 예시
[그림 3]에서 X표시된 곳은 모두 흑돌이 3-3 금수인 경우이며, 헷갈리는 경우는 H10, L14, J4로 이 위치에 흑돌은 착수가 가능하다. H10의 경우에는 3-3이 아닌 4-3으로 가로방향에서 open-4를 만들게 되므로 4-3이다. L14와 J4는 같은 이유에서 3-3이 아닌데, L14의 경우에는 L14에 흑돌을 착수하고 J14나 O14에 흑돌이 착수하여도 한쪽이 막혀있으므로 open-4를 만들지 못해 3이 아니다. 같은 이유에서 J4또한 세로 방향으로 2개의 수로 open-4가 될 수 없으므로 3이 아니므로 금수가 아님을 알 수 있다.
2. Approach
2.1 Flow of code
주의사항: 코딩 리포트의 경우 정말 꼭 필요한 경우가 아니라면 C++ raw code를 리포트에 넣지 않으려고 했기에 가독성이 좀 떨어질수도 있다.
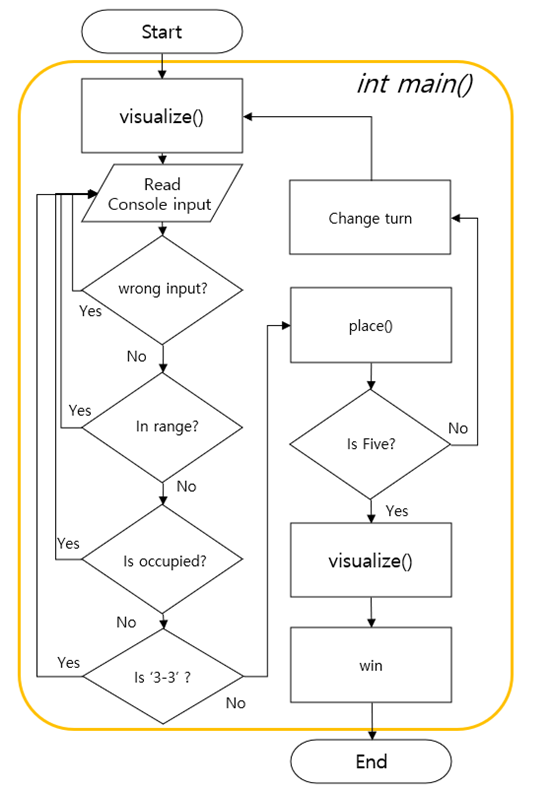
먼저, main 함수의 전체적인 flow는 다음과 같다.
[그림 4] main 함수의 flow chart
먼저, visualize() 함수는 콘솔 창에 오목 판을 표시해주는 함수이며, 이를 거친 뒤 흑돌 먼저 착수하게 된다. 이 때 입력 받은 좌표가 잘못되었거나(wrong input), 범위를 벗어났거나(in range), 이미 돌이 착수된 곳이거나(is occupied), 혹은 ‘3-3’ 조건을 만족하는지(is ‘3-3’) 확인하여 만약 이 중 하나라도 걸리는 부분이 있다면 다시 input을 받는다. 모든 조건을 만족한다면 해당 수를 착수하여 승리하는지(is five) 확인하고, 착수하게 된다. 마지막 수가 아닌 일반적인 경우에는 착수 후 턴을 바꾸어 visualize() 하고, 다시 상대의 입력을 받게 되며, 게임을 끝내는, 즉 5를 만드는 수의 경우 착수, visualize() 이후 win() 함수를 통해 승리했음을 콘솔에 출력 후 함수를 종료한다.
2.2 main 함수의 구성
main 함수의 경우 특정 조건들을 만족할 때까지 계속 입력을 받고, 게임을 승리하였을 경우 프로그램이 종료되어야 하므로, do-while문을 이용하였다. do() 부분에서는 콘솔로부터 입력을 받고, while조건문에 interpret_and_Place()라는 bool return type의 함수를 넣어, 앞서 언급한 모든 조건들을 만족하였다면 해당 함수 내부에서 착수하고 다시 do {} 부분의 block으로 이동할 수 있게 하며, 그렇지 않을 경우 while(false)가 되어 다시 입력을 받도록 하였다. 단, 편의성을 위해 백돌의 차례일 때와 흑돌의 차례일 때를 나누어 각각 2개의 do-while문을 적용하였다.
2.3 ‘3-3’ 함수의 구성
특정 자리에 대해 3-3의 여부를 판별하기 위해서는 ‘상하’, ‘좌우’, ‘좌상-우하’, ‘우상-좌하’의 4가지 방향에 대해서 ‘3’의 여부를 판별해야 한다. 특정 자리에 대해 총 8가지 방향으로, ‘3’의 판별에 유의미한 위치까지 탐색한다. 우선, 8가지 방향에 대해 최대 1개의 빈 공백과, 돌의 끝부분이 보드의 경계나 적의 돌에 의해 막히지 않았는지를 확인한 다음 유효한 돌의 개수를 반환한 다음, 서로 반대 방향끼리 돌의 개수를 합친다. 이렇게 탐색하였을 때 ‘3’이 만족될 경우 count를 1 증가시키고, count가 2 이상일 경우 ‘3-3’ 자리로 판별하게 된다. 이 때 ’3’인 경우만을 엄밀하게 가려내기 때문에 ’4’인 경우에는 ’3’으로 보지 않는다.
Five-in-a-row 판별 함수의 구성
특정 자리에 대해 3-3의 여부를 판별하기 위해서는 ‘상하’, ‘좌우’, ‘좌상-우하’, ‘우상-좌하’의 4가지 방향에 대해서 ‘3’의 여부를 판별해야 한다. 특정 자리에 대해 총 8가지 방향으로, ‘3’의 판별에 유의미한 위치까지 탐색한다. 우선, 8가지 방향에 대해 최대 1개의 빈 공백과, 돌의 끝부분이 보드의 경계나 적의 돌에 의해 막히지 않았는지를 확인한 다음 유효한 돌의 개수를 반환한 다음, 서로 반대 방향끼리 돌의 개수를 합친다. 이렇게 탐색하였을 때 ‘3’이 만족될 경우 count를 1 증가시키고, count가 2 이상일 경우 ‘3-3’ 자리로 판별하게 된다. 이 때 ’3’인 경우만을 엄밀하게 가려내기 때문에 ’4’인 경우에는 ’3’으로 보지 않는다.
3 Data and Procedure
3.1 Input error handling
잘못된 입력을 Handling 하는 부분 main()함수와 밀접히 관련되어 있기 때문에 먼저 main()함수를 설명하고자 한다. 먼저 main() 내부에 bool 변수 isGameOver를 정의하고, 이 값이 false일 동안 계속 input값을 확인하고 착수하는 코드를 while문 내부에서 돌린다. while문 내에서는 일단 visualize()로 시각화 하고, turn이 흑돌일 때와 백돌일 때(흑돌 : -1, 백돌 : 1) 에 대해서 각각 do-while()문을 입력받게 된다. do {} 에서는 입력을 받게 되며, while()문 내부의 조건문에는 interpret_and_Place라는 bool을 return하는 함수가 들어가게 되는데, 해당 함수에 대한 설명은 다음과 같다.
| 함수 명 | interpret_and_place |
|---|---|
| 입력 | int boardinput[][BOARD_SIZE], string userInput, int whosTurn, bool& isGameOver |
| 출력 | bool |
| 설명 | 앞서 언급했던 4가지 조건 (wrong input, out of border, occupied, ‘3-3’)을 만족시킬 경우 false를, 그렇지 않을 경우 true를 반환한다. |
undefined [표 1] interpret_and_place 함수의 입출력과 설명문
먼저, input이 없는 4개의 함수(wrongInput, outOfRange, placeOccupied, doubleThree)은 단순히 콘솔 메시지를 출력하는 함수이다.
interpret_and_place 함수에서는 먼저 userInput의 크기가 4이상이거나 1 이하일 때는 wrongInput()을 호출하고 false를 반환한다. 입력 데이터는 ‘a1’, ‘o15’와 같이 ‘a’ ~ ‘o’까지의 소문자 한글자와 ‘1’ ~ ’15’의 정수가 합쳐진 string의 형태로 전달되므로, userInput[0]에서 char ’a’를 뺀 값을 int col에 저장하게 될 경우 a가 입력되면 0, b는 1, 이런 식으로 o는 15가 col에 입력되게 된다.
한편 row의 경우에는 한자리 수일 수도, 두 자리 수일 수도 있기 때문에 string의 substr() 함수를 이용하여 0번째 index를 제외한 나머지 부분을 모두 row값에 대입한다. 이 때 string을 int로 변환하는 stoi() 함수를 이용하여 int로 변환한다. 또, 0번째 index부터 시작하는 C++과는 달리 오목판은 1부터 시작하므로 1을 빼주어 오목판에서의 1행이 코드 내에서 0번째 행으로 대응되도록 하였다. 최종적으로 row 값에 대한 처리 코드는 다음과 같다 :
1
row = stoi(userInput.substr(1)) - 1;
이 때 userInput의 뒤쪽 부분이 정수가 아닌 다른 값이 입력될 경우 stoi() 자체에서 exception을 발생시키므로, try - catch문을 이용하여 exception이 발생할 경우 wronginput으로 간주하도록 하였다. 이렇게 만들어진 최종 코드는 다음과 같다:
1
2
3
4
5
6
7
try {
row = stoi(userInput.substr(1)) - 1;
}
catch (const exception& e) {
wrongInput();
return false;
}
추가적으로 대문자나 다른 1byte char가 입력되게 된 경우 col의 값이 0보다 작거나 26보다 커질 수도 있다. 이 때는 wrong input으로 취급한다.
또한 문제 조건에 의해 ‘p’ ~ ’z’의 문자열이 입력된 경우는 wrong input이 아닌 out of border 에러로 간주하게 되므로, 0< row < BOARD_SIZE 조건과 더불어 out of range 문구를 띄우게 된다.
만약 또한 (row, col)의 자리가 0이 아닌 경우에는 다른 돌이 이미 놓아져 있는 경우이므로, placeOccupied() 함수를 호출하고 false를 반환한다. 마지막으로, 현재의 차례가 X(흑)의 차례이고, ’3-3’조건을 만족하는 경우 (isDoubleThree() 함수에서 true가 반환된 경우) doubleThree() 함수를 호출하고 false를 반환한다.
다음으로 place()함수로 착수하고, 5-in-a-row를 완성했는지 확인한 다음, 완성되었다면 win() 함수를 출력하여 승자를 출력하고 종료, 그렇지 않다면 true를 출력하게 된다.
main 함수에서 while(!interpret_and_place() ) 로 입력되어 있어 해당 함수에서 false가 출력되면 다시 do{}의 코드블럭을 수행하게 되며 true가 출력될 경우 탈출하여 다음 사람에게로 turn이 넘어간다.
3.2 ‘3-3’ 판별 함수의 구현
’3-3’을 확인하기 위해서 총 2개의 함수를 이용하여 구현하였는데, 두 함수에 대한 설명은 다음과 같다.
| 함수 이름 | assignDirection |
|---|---|
| 입력 | int& row, int& col, int direction |
| 출력 | void |
| 설명 | 0~7까지의 direction 입력에 대해 row, col값을 바꾸어 준다. 예를 들어 1의 경우 NW 방향이므로 row–, col–를 실행한다. |
undefined [표 2] assignDirection 함수의 입출력과 설명
| 함수 이름 | search |
|---|---|
| 입력 | int boardsize[][BOARD_SIZE], int row, int col, int direction, int&space, int&cnt, int mystone |
| 출력 | int |
| 설명 | 8가지 방향에 대해 다음 제약 조건들을 모두 통과시키는 경우 탐색을 진행한다: 1. 탐색하고자 하는 칸이 보드를 벗어난 경우 2. 2칸의 연속된 빈칸이 존재한 경우 3. 한칸짜리 빈칸이 2개 이상 발견된 경우 4. 탐색하고자 하는 칸에 상대방의 돌(백돌)이 있는 경우 이 4가지 조건을 만족시킬 경우 다음 칸을 탐색한다. 이 때 탐색하고자 하는 칸이 흑돌인 경우 cnt 또한 증가시킨다. 앞선 4가지 조건 중 하나라도 만족시키지 못할 경우 탐색을 종료하고 cnt값을 반환한다. |
undefined [표 3] search 함수의 설명
search 함수는 위 설명과 같이 작동되며, 특히 space와 cnt의 경우에는 해당 돌을 기준으로 서로 반대되는 방향에 대해 공통적으로 적용되는 변수이므로 reference로 하여 값을 공유하게 하였다.
함수 내에서 정의된 지역변수들의 목록과 그 정의는 다음과 같다:
int cnt : 연결된 흑돌의 개수를 세어 출력한다.
int& space : 허용되는 한 칸 짜리 빈칸의 개수로, 현재 착수할 위치의 빈칸을 제외하고 최대 1개의 빈칸이 허용되므로 space는 0으로 초기화 되어 입력된다. search 함수 내의 탐색하는 알고리즘은 모두 space가 1 이하일 때 라는 while문 내부에 위치하므로 space가 2가 되는 순간 자동으로 탐색을 종료하게 된다. 또한 연속된 2개의 빈칸의 경우에는 space를 2번 더하는 것이 아니라 space는 더하지 않고 탐색만 종료하는 것이 옳으므로 이를 고려해 주었다.
bool doublespace : 처음에 false 상태로 initialize 되어 처음 빈칸을 만나면 true가 되고, true인 상태에서 한 번 더 빈칸을 만나면 변수의 이름 그대로 연속된 두 칸을 만난 것이므로 탐색을 종료한다. 연속된 빈칸이 아니라 다시 원래대로 흑돌(X)이 나올 경우 doublespace를 false로 돌려준다.
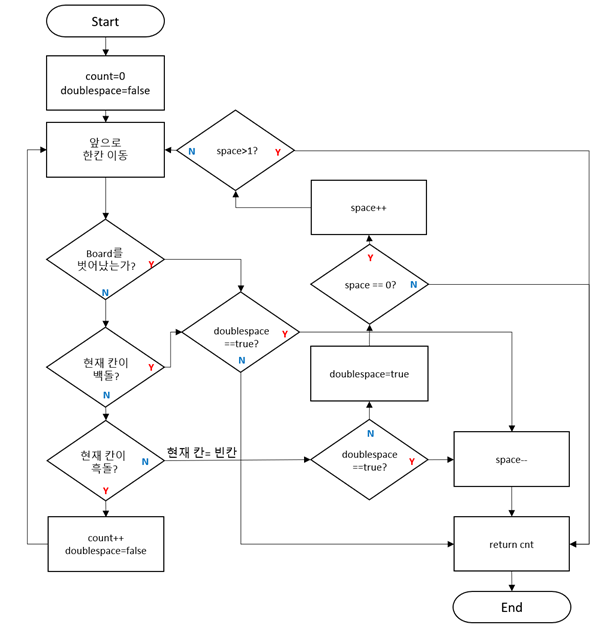
[그림 5] search 함수의 flow chart
[그림 5]를 조금 더 풀어서 설명하고자 한다. 먼저 지정된 방향으로 한 칸 이동한 다음, Board를 벗어나거나 현재 칸이 백돌인 경우에는 함수를 탈출한다. 현재 칸이 흑돌인 경우에는 count 값을 하나 올리고 다음 칸을 탐색한다. 만약 현재 칸이 빈칸인 경우, 그 중에서도 doublespace가 false인 경우에는 바로 직전 칸이 빈칸이 아닌 경우이므로, 먼저 doublespace를 true로 바꾸어 준다. Space가 0이라면, 즉 이번 전체 탐색에서 한칸짜리의 빈칸이 한번도 기록되지 않은 경우 space값을 늘려 유효한 빈칸임을 표시하며 space가 0이 아니라면 탐색을 종료한다. (이미 한칸의 빈칸이 포함되었는데 또다른 빈칸을 만났으므로)
다시 탐색을 하다 Board를 벗어나거나 백돌이 발견되는 경우 그 직전 칸이 빈칸이었다면 해당 빈칸은 올바른 한 칸짜리 빈칸이 아니므로 다시 space를 되돌려주고 탐색을 종료하게 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int search(int boardinput[][BOARD_SIZE], int row, int col, int direction, int& space, int mystone) {
bool doublespace = false;
int cnt = 0;
while (space <= 1) {
assignDirection(row, col, direction);
if (row >= BOARD_SIZE || row < 0 || col >= BOARD_SIZE || col < 0) {
if (doublespace) {space--;}
break;
}
else if (boardinput[row][col] == -mystone) { // ~~ == O
if (doublespace) {space--;}
break;
}
else if (boardinput[row][col] == mystone) { // ~~ == X
cnt++;
doublespace = false;
}
else { // space (boardinput[row][col] == 0)
if (!doublespace) {doublespace = true;}
else { // double space : exit
space--;
break;
}
if (space == 0) {space++;}
else {break;}
}
}
return cnt;
}
| 함수 이름 | isDoubleThree |
|---|---|
| 입력 | int boardsize[][BOARD_SIZE], int row, int col |
| 출력 | bool |
| 설명 | search함수에 의해 각 방향을 탐색하고, 탐색이 종료된 지점 바로 다음 위치를 조사하여 open-4 조건을 만족하는지 확인한다. |
undefined [표 4] isDoubleThree 함수의 설명
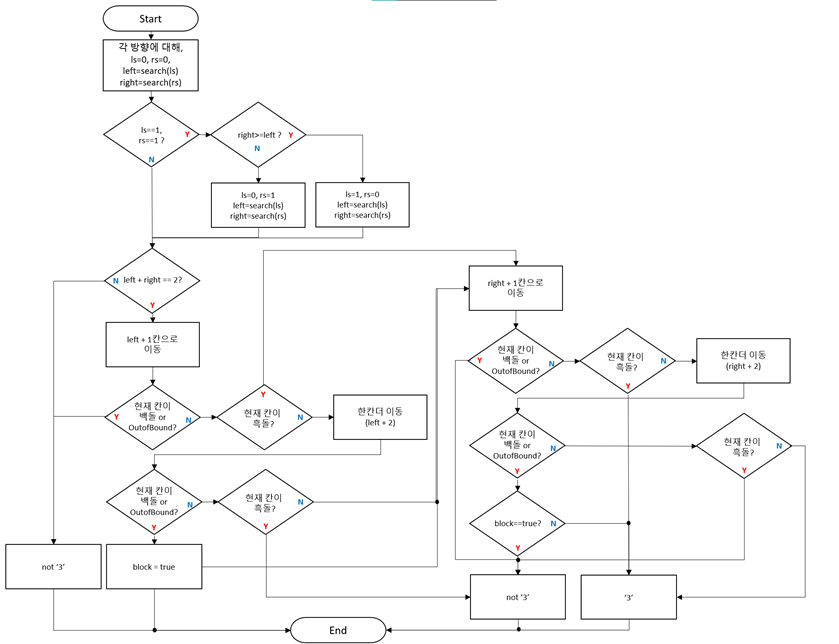
8가지 방향 중 서로 반대되는 방향끼리 짝지어 4개의 방향으로 좁혀지는데, 이 때 각각에 대해 leftspace, rightspace=0을 대입한 상태에서 search() 함수의 결과를 left와 right에 저장한다. 이렇게 되면 최대로 space를 가지는 경우 leftspace = 1, rightspace = 1인 경우가 생길 수 있다. 이 때 (X - * - X X)에서 (X 흑돌, - 빈칸, * 현재 착수하려는 빈칸) * 칸에 착수하게 될 경우 3이 됨이 명백하지만, count가 3이 되어 ’4’로 인식하게 된다. 이렇게 양쪽에서 space를 모두 사용한 경우에는 흑돌의 배치가 더 많은 한쪽의 빈칸을 이용하고 반대편을 버려야 한다. 그러므로 left와 right의 크기를 비교하고 right이 큰 경우 leftspace를 1로 초기화한 다음 대입하여 left쪽에서 생기는 space를 무시, 반대로 left이 큰 경우 rightspace를 1로 초기화한 다음 대입하여 right에서 생기는 space를 무시하는 식으로 구현하였다.
최종적으로 구해진 left와 right의 합이 2라면 left쪽과 right쪽이 ’열린 상태’인지를 확인해야 한다. 왼쪽의 끝부분은 왼쪽에 놓인 흑돌의 개수 + 왼쪽에서 사용된 space의 개수이므로 이를 더하여 이동시켜주고 해당 칸의 열림 여부를 판단한다. 같은 방법으로 오른쪽의 끝부분은 오른쪽에 놓인 흑돌의 개수 + 오른쪽에서 사용된 space의 개수이므로 이를 더하여 이동하고 해당 칸의 열림을 확인한다.
‘열림’ 여부를 확인하는 방법은 개념만 잘 이해한다면 어렵지 않다. 먼저 마지막 칸 다음 칸이 오목판의 경계이거나 백돌이라면 당연히도 막혀있는 경우이므로 그대로 continue;를 통해 다음 방향을 탐색하면 된다. 다음칸이 흑돌인 경우가 있는데, 이는 앞서 처리한 (leftspace =1, rightspace=1)인 경우에만 나타난다. 앞서 해당 경우에는 돌의 수가 더 작은쪽 방향의 space를 무시하기로 하였으므로 이 경우 에는 흑돌을 없는 돌 취급하고 계속 조사하면 된다. 예시를 들자면, (X - * - X X)의 경우인데, 마지막으로 조사한 칸이 왼쪽에서 2번째 칸이므로 첫번째 칸인 X가 나왔을 때 단순히 X를 – 취급하여 무시하면 된다.
만약 마지막 다음칸이 빈칸일 경우, 한 칸을 더 조사해 보아야 한다. 그 다음칸이 흰돌이나 판의 경계선으로 막혀있다면, 이 상태는 ’반쯤 막힌 상태’가 될 것이다. 그러므로 blocked를 true로 바꾸어 준다. 반대쪽도 같은 방법으로 조사하여 양쪽 모두가 반쯤 막힌 상태라면, 현재 배치는 (O – X * X – O ) 상태일 것이다. * 위치는 ’3’처럼 보이지만 양쪽이 막혀 있어 사실 열린 3이 아니다. 이러한 경우를 판별하기 위해 block 변수를 두고 양쪽 모두가 반쯤 막힌 상태일 때 continue;로 빠져나가는 것이다.
[그림 6] isDoubleThree 함수의 flow chart
3.3 Five-in-a-row 판별함수의 구현
5개가 연속적으로 놓여있는지를 확인하는 함수를 종전에 따로 구현하였었지만, ’3-3’을 구현하고 search 함수를 이용하여 조금 더 명확하고 줄 수를 줄일 수 있겠다는 생각이 들어 search함수의 매개변수를 조금 변형시켜 5-in-a-row 함수를 구현하였다. 오목을 판정하는 함수는 이미 돌이 착수된 이후에 시행되는 함수이므로, 해당 위치에 이미 돌이 놓아져 있다고 간주해도 상관이 없다. isFive 함수는 지정된 위치 주변 4개 방향 (상하/좌우/대각선/역 대각선) 각각에 대해 space=1로 두고 search()를 진행하여 cnt의 합이 4보다 커지는 경우 true를 반환하도록 하였다. search함수에서 space가 2 이상이면 바로 함수가 종료되는 점에서 착안하여 애초에 space 값에 1을 넣어주었다. 이렇게 되면 벽을 만나거나, 상대편 돌을 만나거나, 빈 공간을 만나는 그 어떤 경우에도 search가 종료되게 된다. 이렇게 하면 굳이 4가지 방향에 대해 동일한 코드를 반복할 필요 없이 이미 구현한 코드인 search()를 매개변수만 바꾸어 재사용하여 코드의 간결성을 확보할 수 있다.
4. Result
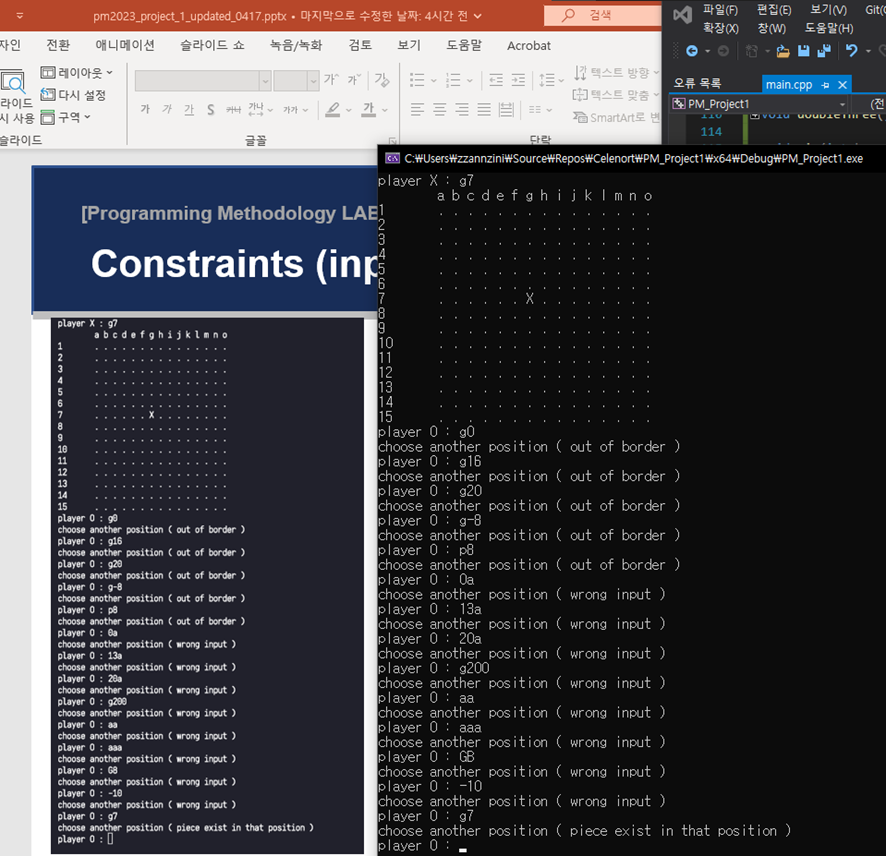
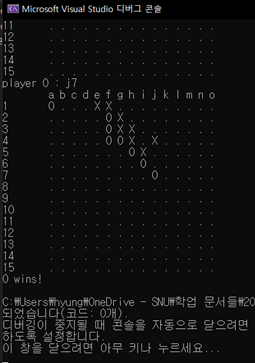
4.1 Input Error Handling
[그림 7] Input Error Handling
그림과 같이 주어진 예시 자료와 동일하게 input error를 처리하는 모습을 확인할 수 있다.
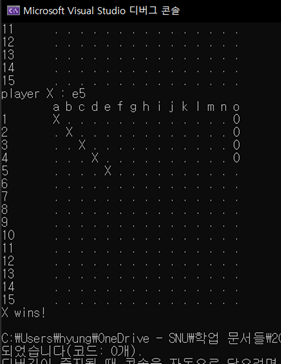
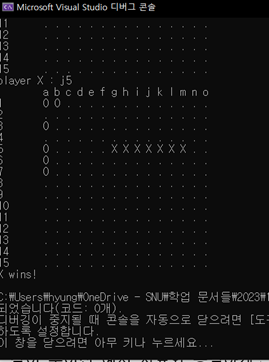
4.2 Five-in-a-row detection
그림과 같이5-in-a-row가 발생하면 정확히 detecting하는 것을 확인할 수 있다.
[그림 8] 5-in-a-row detection을 수행하는 모습.
[그림 8]과 같이 흑이나 백의 5-in-a-row를 제대로 catch하는 모습을 알 수 있다. 가장 오른쪽의 예시에서 알 수 있듯이 장목(6목 이상)의 제약조건이 없기에 이러한 경우에도 5목을 정확히 판별함을 알 수 있다.
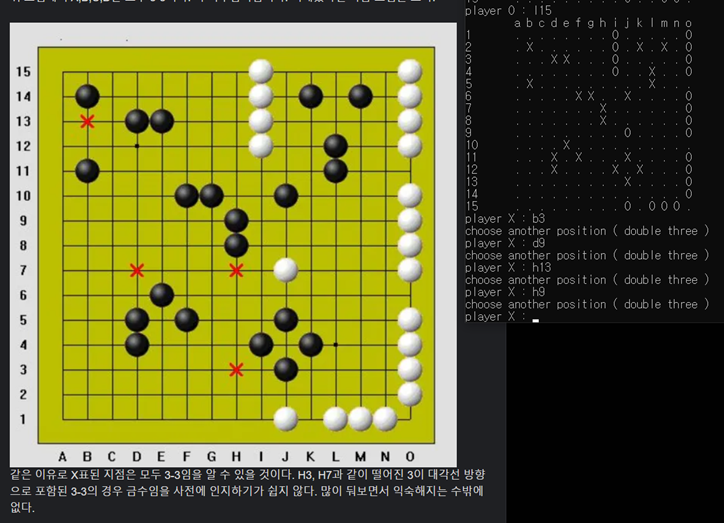
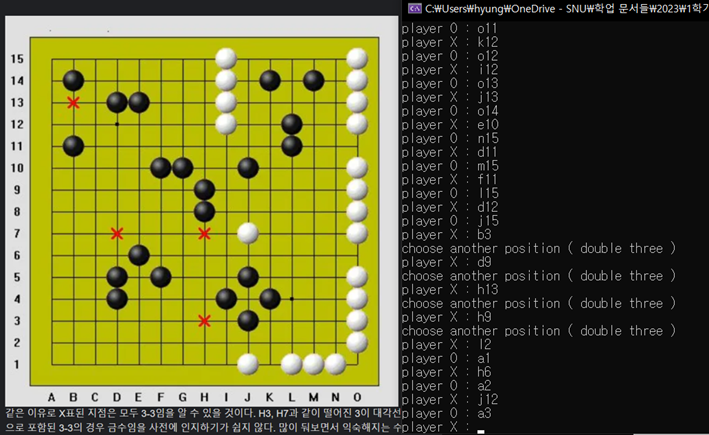
4.3 ‘3-3’ detection while allowing ‘4-3’, ‘4-4’
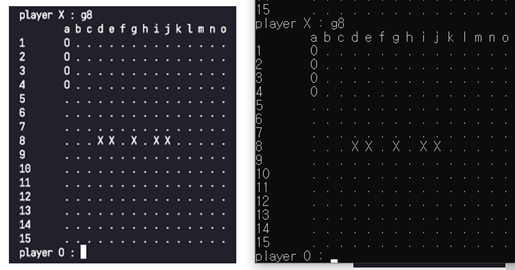
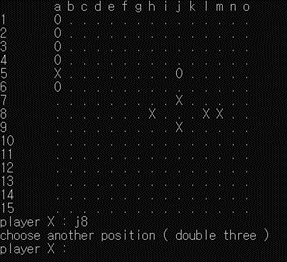
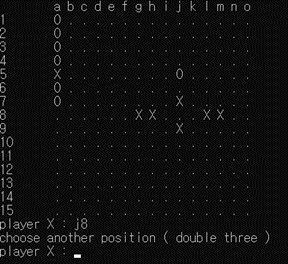
[그림 9] ’3-3’을 정확하게 구분하는 모습
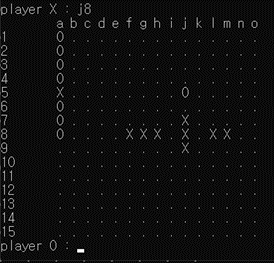
[그림 9]에서 알 수 있듯이 b3, d9, h13, h9에 대해 금수 자리를 정확히 파악하고 double three 에러를 띄우는 모습이다. ([그림 9]에서 오목판의 경우 행 번호 indexing이 반대여서 헷갈릴 수 있으나 16-행번호 로 두 관계를 변환할 수 있다.) 이 때 l2, h6, j12와 같은 점들은 금수처럼 보이지만 ’3-3’이 아니어서 금수가 아니기 때문에 해당 자리에는 착수가 가능함을 알 수 있다.
[그림 10] l2, h6, j12 자리에 착수가 가능함.
다음은 Project의 PPT 파일에 실린 Confusing case를 테스트해 보았다.
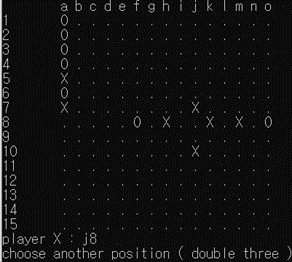
[그림 11] 한쪽 방향으로 2개의 3이 생기는 경우
한쪽 방향(좌우) 로 2개의 3이 생기는 경우는 ‘3-3’ 조건이 아니므로 정상적으로 착수된 것을 알 수 있다.
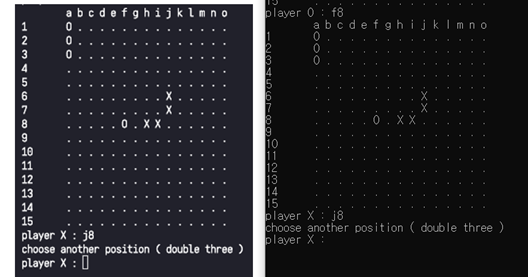
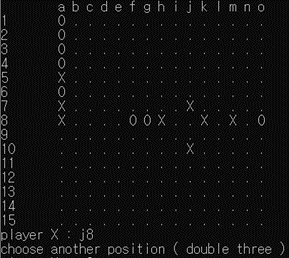
[그림 12] ‘semi-open-4’에 대한 ‘3-3’
[그림 12]의 경우 가로 방향으로 f8에 의해 한쪽이 막혔지만, 다른 한쪽이 열려있어 open-4 조건을 만족하므로, ‘3-3’ 금수에 의해 착수가 불가능함을 알 수 있다.
[그림 13] ‘closed-4’에 대한 ‘3-3’
[그림 13]을 보면 g8, m8에 의해 가로 방향이 완전히 막혀있음을 알 수 있다. 이 경우 착수하여도 세로 방향을 먼저 막은 다음, 막을 길이 존재하므로(즉 무적수가 아니므로) ‘3-3’ 금수 조건에 어긋난다. 그러므로 착수가 가능함을 알 수 있다.
[그림 14] 한 방향으로 ’3’이 2개 인식가능 할 때의 처리
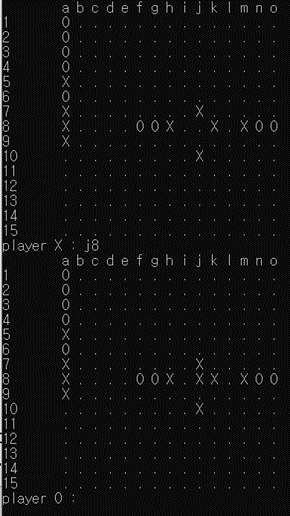
[그림 14]는 [그림 11]과 비슷해 보이지만 조금 다름을 알 수 있다. 가장 왼쪽의 그림을 보면, 가로 방향으로 j8자리에 착수하였을 때 l8,m8에 의해 ‘3’이 만들어져 ‘3-3’임을 알 수 있다. 그렇다면 가운데 그림에서와 같이 한 방향으로 2개의 ‘3’이 만들어지는 경우를 제대로 처리하는지 확인해 보면, 이 때 또한 ‘3-3’ 처리를 함을 알 수 있다. 마지막으로, f8에 흑돌을 두어 j8에 두었을 때 ‘4’가 만들어지도록 하면, 그제서야 j8에 착수가 가능해진 것을 알 수 있다. (‘4-3’ detection)
[그림 15] 연결되어 있지 않은 돌들에 대한 ‘open-4’ 처리
[그림 15] 또한 pitfall에 빠질 수 있는 예제로, 좌측 상단 그림을 보았을 때 가로 방향으로 h8, k8이 ‘3’을 만들기 때문에 j8 자리가 ‘3-3’ 금수이다. (혹은, k8, n8도 ’3’을 만들기 때문에 금수라고 볼 수 도 있는데, 이는 [그림 14]의 예와 동일한 문제이다.) 이 때 좌측 하단 그림처럼 g8을 막아 h8, k8이 더 이상 ’3’을 만들 수 없도록 한다면 어떻게 될까? 각 방향에서 단 한 개의 ’3’만을 탐색하여 바로 빠져나오게 된다면 착수 가능한 자리라고 판정할 수도 있다. 그러나 h8, k8이 ’3’을 만들지 못하더라도 k8, m8에 의해 여전히 가로 ’3’을 만들 수 있으므로 j8은 여전히 금수이다. 마지막으로 우측 그림에서 처럼 n8까지 막혀 가로 방향의 어느 두 흑돌로도 ’3’을 만들 수 없을 때에는 j8의 금수가 풀려 착수가 가능함을 알 수 있다.
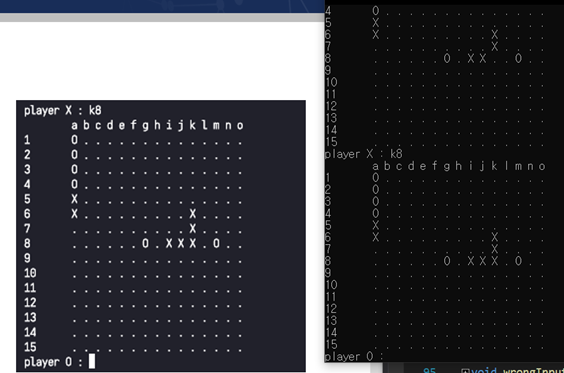
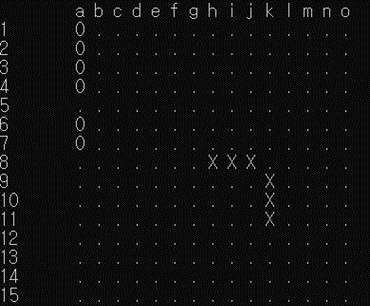
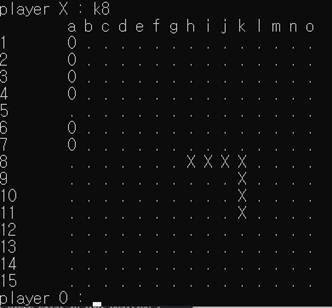
[그림 16] ‘4-4’ exception 처리
[그림 16] 에서 알 수 있듯이 자칫 ‘3-3’ 금수로 취급될 수 있는 ‘4-4’ 또한 금수 자리가 아니기 때문에 k8에 정상적으로 착수 가능함을 확인할 수 있다.
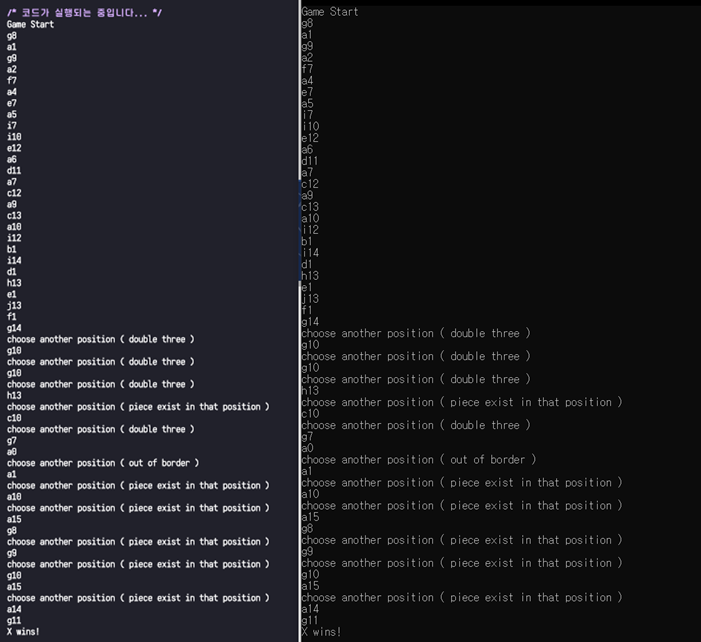
[그림 17] 최종적인 출력 파일
[그림 17]을 통해 elice에서 실행된 예제와 제작한 C++ 콘솔창이 완벽히 동일한 동작을 보임을 알 수 있다.
5. Discussion
- 아파서 여기 부분은 쓰지도 못했음…
- 어차피 특정 좌표는 총 3가지의 상태를 갖는다. 백/흑/착수되지 않음(빈공간)
- 그렇다면 3-3/4-3은 총 현재 관심을 가지고 있는 돌을 기준으로 8가지 방향(반대방향끼리 묶으면 4가지 방향)에 대해서 한정된 가짓수의 상태만을 갖는다.
- ’4-4’라는 최대 경우를 생각해봐도 현재 착수하려는 위치의 상하좌우 대각선 포함 4개 앞뒤의 돌까지만 관심이 있으므로, 한가지 방향에 대해 착수위치를 가운데로 두고 9개의 위치의 돌만을 확인하면 된다.
- 계산해 보면 38가짓수를 가질 수 있다는 것이고, 백/흑이 서로 바뀐 상황, 착수 불가능한 상황 등을 다 제외하면 훨씬 줄어들 것이다.
- 이에 대해 하드코딩으로 코딩을 하게 되면, 코딩 자체는 엄청 길어지겠지만 (각 경우에 대한 판별을 dictionary 형식으로 저장) 연산속도의 경우 착수위치 주변 많아봐야 32개의 위치를 조사하여 바로 결과가 나오게 할 수 있을 것이다.
- 추가적으로, class나 struct와 같은 객체의 사용이 금지된 과제여서 사용을 못했지만 class에 메서드를 입력받아서 하는 식으로 하면 더 간단하고 직관적으로 구현이 가능했을 것으로 보인다.
What is Renju? - https://www.renju.net/rules/ ↩︎